题目内容
已知![]() ,
,
且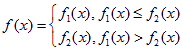 .
.
(Ⅰ)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
![]() (Ⅱ)当
(Ⅱ)当![]() 时,设
时,设![]() 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为![]() (闭区间
(闭区间![]() 的长度定义为
的长度定义为![]() ),试求
),试求![]() 的最大值;
的最大值;
![]() ,当
,当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() ,
,
解析:
解: (Ⅰ)当![]() 时,
时,![]() .
.
因为当![]() 时,
时,![]() ,
,![]() ,
,
且![]() ,
,
所以当![]() 时,
时,![]() ,且
,且![]() ……………………(5分)
……………………(5分)
由于![]() ,所以
,所以![]() ,又
,又![]() ,
,
故所求切线方程为![]() ,
,
即![]() ………………………………………………(8分)
………………………………………………(8分)
(Ⅱ) 因为![]() ,所以
,所以![]() ,则
,则
① ![]() 当
当![]() 时,因为
时,因为![]() ,
,![]() ,
,
所以由![]() ,解得
,解得![]() ,
,
从而当![]() 时,
时,![]() …………………………(10分)
…………………………(10分)
② 当![]() 时,因为
时,因为![]() ,
,![]() ,
,
所以由![]() ,解得
,解得![]() ,
,
从而当![]() 时,
时,![]() ………………………(12分)
………………………(12分)
③当![]() 时,因为
时,因为![]() ,
,
从而![]() 一定不成立…………………………………………(14分)
一定不成立…………………………………………(14分)
综上得,当且仅当![]() 时,
时,![]() ,
,
故![]()
从而当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() ……………………………………(16分)
……………………………………(16分)

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 且
且 ,在各项为正的数列
,在各项为正的数列 中,
中, 的前n项和为
的前n项和为 ,若
,若 = 。
= 。 且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在
且此函数图象过点(1,5).(1)求实数m的值; (2)判断f(x)奇偶性;(3)讨论函数f(x)在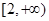 上的单调性?并证明你的结论.
上的单调性?并证明你的结论.