题目内容
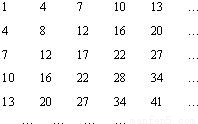
下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为Aij.(1)设S中主对角线上的数1,8,17,28,41,…组成数列{bn}.试证不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列;
(2)对于(1)中的数列{bn},是否存在正整数p和r (1<r<p<150),使得b1,br,bp成等差数列.若存在,写出p,r的一组解(不必写出推理过程);若不存在,请说明理由.
【答案】分析:(1)假设存在k、m,1<k<m,使得b1,bk,bm成等比数列,则根据等比中项的性质可知b1bm=bk2,根据题意bn=Ann=(n+2)2-4;求得(m+2)2-[(k+2)2-8]2=8,同时1<k<m,则可推断k≥2、m≥3,进而可知(m+2)+(k+2)2-8≥13进而可得出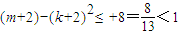 与(m+2)-(k+2)2+8∈Z矛盾,推断出不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列.
与(m+2)-(k+2)2+8∈Z矛盾,推断出不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列.
(2)假设存在满足条件的p,r,则根据等差中项的性质可知2(r2+4r-4)=1+(p2+4p-4),令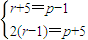 求得p和r.
求得p和r.
解答:解:(1)证明:假设存在k、m,1<k<m,使得b1,bk,bm成等比数列,
即b1bm=bk2,
∵bn=Ann=(n+2)2-4;
∴1×[(m+2)2-8]=[(k+2)2-8]2
得(m+2)2-[(k+2)2-8]2=8,
即[(m+2)+(k+2)2-8][(m+2)-(k+2)2+8]=8,
又∵1<k<m,且k、m∈N,
∴k≥2、m≥3,(m+2)+(k+2)2-8≥5+16-8=13
∴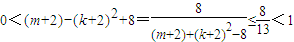 ,这与(m+2)-(k+2)2+8∈Z矛盾,
,这与(m+2)-(k+2)2+8∈Z矛盾,
所以不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列.
(2)解:假设存在满足条件的p,r,那么2(r2+4r-4)=1+(p2+4p-4),
即2(r+5)(r-1)=(p+5)(p-1)
不妨令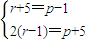
得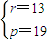
所以存在r=13,p=19使得b1,br,bp成等差数列.
点评:本题主要考查了数列的应用,不等式的证明,等差数列和等比数列的性质.考查了学生综合分析问题和解决问题的能力.
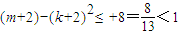 与(m+2)-(k+2)2+8∈Z矛盾,推断出不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列.
与(m+2)-(k+2)2+8∈Z矛盾,推断出不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列.(2)假设存在满足条件的p,r,则根据等差中项的性质可知2(r2+4r-4)=1+(p2+4p-4),令
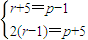 求得p和r.
求得p和r.解答:解:(1)证明:假设存在k、m,1<k<m,使得b1,bk,bm成等比数列,
即b1bm=bk2,
∵bn=Ann=(n+2)2-4;
∴1×[(m+2)2-8]=[(k+2)2-8]2
得(m+2)2-[(k+2)2-8]2=8,
即[(m+2)+(k+2)2-8][(m+2)-(k+2)2+8]=8,
又∵1<k<m,且k、m∈N,
∴k≥2、m≥3,(m+2)+(k+2)2-8≥5+16-8=13
∴
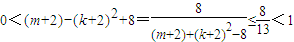 ,这与(m+2)-(k+2)2+8∈Z矛盾,
,这与(m+2)-(k+2)2+8∈Z矛盾,所以不存在正整数k和m(1<k<m),使得b1,bk,bm成等比数列.
(2)解:假设存在满足条件的p,r,那么2(r2+4r-4)=1+(p2+4p-4),
即2(r+5)(r-1)=(p+5)(p-1)
不妨令
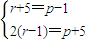
得
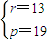
所以存在r=13,p=19使得b1,br,bp成等差数列.
点评:本题主要考查了数列的应用,不等式的证明,等差数列和等比数列的性质.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
相关题目
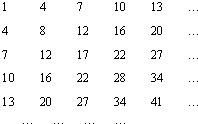 下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为Aij.
下述数阵称为“森德拉姆筛”,记为S.其特点是每行每列都是等差数列,第i行第j列的数记为Aij.