Question

设U={x∈N|x＜10}，若（C_UA）∩（C_UB）={1，9}，（C_UA）∩B={4，6，8}，A∩B={2}，则A∩（C_UB）=________．

Answer 1

{0，3，5，7}
分析：由已知中U={x∈N|x＜10}，若（C_UA）∩（C_UB）={1，9}，（C_UA）∩B={4，6，8}，A∩B={2}，我们可以画出满足条件的韦恩图，由于分析全集U中元素被分成的四部分的元素，即可得到答案．
解答：∵U={x∈N|x＜10}={0，1，2，3，4，5，6，7，8，9}
又∵（C_UA）∩（C_UB）={1，9}，
（C_UA）∩B={4，6，8}，
A∩B={2}，
∴集合A，B，U的元素分配如下图所示

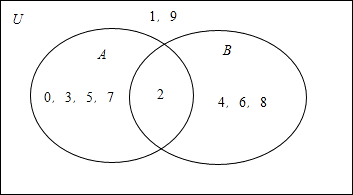
由图可得A∩（C_UB）={0，3，5，7}
故答案为：{0，3，5，7}
点评：本题考查的知识点是集合交、并、补集的混合运算，其中画出满足条件的韦恩图，用数形结合的思想进行解答，是本题的关键．