题目内容
已知虚数z满足等式: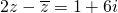 ,则z=________.
,则z=________.
1+2i
分析:设复数 z=a+bi (a、b∈R),根据两个复数相等的充要条件,待定系数法求出a、b的值,从而求出z.
解答:∵虚数z满足等式: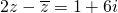 ,∴设复数 z=a+bi (a、b∈R),
,∴设复数 z=a+bi (a、b∈R),
由题意得 (2a+2bi)-(a-bi)=1+6i,a+3bi=1=6i,∴a=1,3b=6,
∴a=1,b=2,∴z=1+2i
故答案为:1+2i.
点评:本题考查两个复数相等的充要条件,用代定系数法求出复数的实部和虚部,从而得到复数的值.
分析:设复数 z=a+bi (a、b∈R),根据两个复数相等的充要条件,待定系数法求出a、b的值,从而求出z.
解答:∵虚数z满足等式:
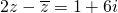 ,∴设复数 z=a+bi (a、b∈R),
,∴设复数 z=a+bi (a、b∈R),由题意得 (2a+2bi)-(a-bi)=1+6i,a+3bi=1=6i,∴a=1,3b=6,
∴a=1,b=2,∴z=1+2i
故答案为:1+2i.
点评:本题考查两个复数相等的充要条件,用代定系数法求出复数的实部和虚部,从而得到复数的值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
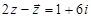 ,则z=
,则z= 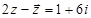 ,则z=
,则z= 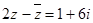 ,则
,则 。
。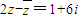 ,则z= .
,则z= .