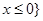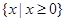题目内容
已知函数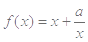 ,且
,且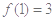 .
.
(1)求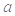 的值,并确定函数
的值,并确定函数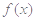 的定义域;
的定义域;
(2)用定义研究函数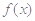 在
在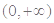 范围内的单调性;
范围内的单调性;
(3)当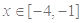 时,求出函数
时,求出函数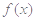 的取值范围.
的取值范围.
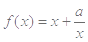 ,且
,且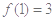 .
.(1)求
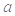 的值,并确定函数
的值,并确定函数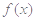 的定义域;
的定义域;(2)用定义研究函数
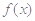 在
在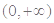 范围内的单调性;
范围内的单调性;(3)当
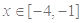 时,求出函数
时,求出函数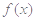 的取值范围.
的取值范围.(1)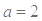 ,定义域:
,定义域: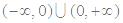 ;(2)
;(2)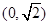 上是减函数,
上是减函数,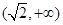 上是增函数;
上是增函数;
(3)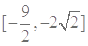 .
.
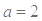 ,定义域:
,定义域: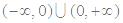 ;(2)
;(2)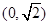 上是减函数,
上是减函数,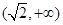 上是增函数;
上是增函数;(3)
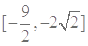 .
.试题分析:(1)直接代入列出关于
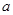 的方程即可;(2)要正确理解单调性的定义,明确用定义研究(或证明)函数的单调性的格式过程,设
的方程即可;(2)要正确理解单调性的定义,明确用定义研究(或证明)函数的单调性的格式过程,设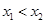 ,然后比较
,然后比较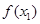 和
和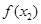 的大小,通常是作差
的大小,通常是作差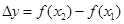 (也可
(也可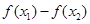 ),确定差的正负;(3)由(2)中的单调性,可容易求出函数的取值范围.
),确定差的正负;(3)由(2)中的单调性,可容易求出函数的取值范围.试题解析:(1)
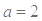 ,定义域:
,定义域: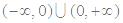 ; 3分
; 3分(2)令
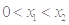 ,则
,则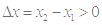 ,
,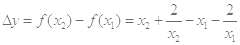
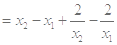
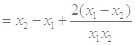
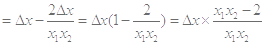 6分
6分故当
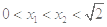 时,
时,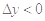 ;当
;当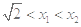 时,
时,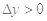 ,
,∴函数
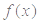 在
在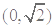 上单调减,在
上单调减,在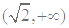 上单调增; 8分
上单调增; 8分(3)由(2)及函数
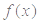 为奇函数知,函数
为奇函数知,函数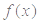 在
在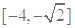 为增函数,在
为增函数,在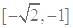 为减函数,故当
为减函数,故当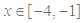 时,
时,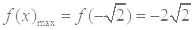 , 10分
, 10分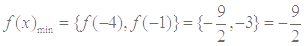 ,
,∴当
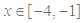 时,
时,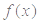 的取值范围是
的取值范围是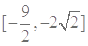 . 12
. 12
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
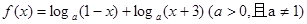
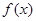 的定义域和值域;(2)若函数
的定义域和值域;(2)若函数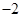 ,求
,求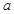 的值。
的值。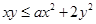 对于
对于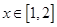 ,
,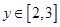 恒成立,则实数
恒成立,则实数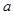 的取值范围是____________.
的取值范围是____________.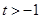 ,当
,当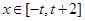 时,函数
时,函数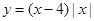 的最小值为-4,则
的最小值为-4,则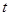 的取值范围是________.
的取值范围是________.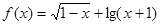 的定义域是 .
的定义域是 .  的值域为______________.
的值域为______________.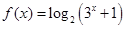 的值域为 .
的值域为 .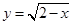 的定义域为( )
的定义域为( )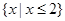
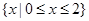
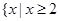 或
或