题目内容
 如图为一个观览车示意图,该观览车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离为h.
如图为一个观览车示意图,该观览车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离为h.(1)在如图所示直角坐标系中,求h与θ间关系的函数解析式;
(2)设从OA开始转动,经过t秒到达OB,求h与t间关系的函数解析式;
(3)填写下列表格:
| θ | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| h(m) |
| t(s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| h(m) |
分析:(1)过点O作地面平行线ON,过点B作ON的垂线BM交ON于M点.当θ>
时,∠BOM=θ-
.|BM|=8sin(θ-
),即可得出h=|OA|+0.8+|BM|.当0≤θ≤
时,上述关系式也适合.
(2)点A在⊙O上逆时针运动的角速度是
=
,t秒转过的弧度数为
t,即可得出.
(3)利用h=4.8sin(
t-
)+5.6,分别令t=0,5,10,15,20,25,30即可得出h(t).同理利用h=4.8sin(θ-
)+5.6可得h(m).
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)点A在⊙O上逆时针运动的角速度是
| 2π |
| 60 |
| π |
| 30 |
| π |
| 30 |
(3)利用h=4.8sin(
| π |
| 30 |
| π |
| 2 |
| π |
| 2 |
解答:解:(1)过点O作地面平行线ON,过点B作ON的垂线BM交ON于M点.
当θ>
时,∠BOM=θ-
.h=|OA|+0.8+|BM|=5.6+4.8sin(θ-
).
当0≤θ≤
时,上述关系式也适合.
∴h=4.8sin(θ-
)+5.6.
(2)点A在⊙O上逆时针运动的角速度是
=
,
∴t秒转过的弧度数为
t.
∴h=4.8sin(
t-
)+5.6,t∈[0,+∞).
(3)利用h=4.8sin(
t-
)+5.6,分别令t=0,5,10,15,20,25,30即可得出h(t).
同理利用h=4.8sin(θ-
)+5.6,即可得出h(m).

当θ>
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
当0≤θ≤
| π |
| 2 |
∴h=4.8sin(θ-
| π |
| 2 |
(2)点A在⊙O上逆时针运动的角速度是
| 2π |
| 60 |
| π |
| 30 |
∴t秒转过的弧度数为
| π |
| 30 |
∴h=4.8sin(
| π |
| 30 |
| π |
| 2 |
(3)利用h=4.8sin(
| π |
| 30 |
| π |
| 2 |
同理利用h=4.8sin(θ-
| π |
| 2 |
| θ | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
| h(m) | 0.8 | 1.4 | 3.2 | 5.6 | 8.0 | 9.8 | 10.4 |
| t(s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| h(m) | 0.8 | 1.4 | 3.2 | 5.6 | 8.0 | 9.8 | 10.4 |
点评:本题考查了三角函数的图象与性质、数形结合等基础知识与基本技能方法,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
下图为一个观览车示意图,该观览车半径为4.8 m,图上最低点与地面距离为0.8 m,60 s转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离为h.
(1)求h与θ间关系的函数解析式;
(2)设从OA开始转动,经过t秒到达OB,求h与t间关系的函数解析式;

(3)填写下列表格:
θ | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
h(m) |
|
|
|
|
|
|
|
t(s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
h(m) |
|
|
|
|
|
|
|
下图为一个观览车示意图.该观览车圆半径为4.8 m ,圆上最低点与地面距离为0.8 m ,60秒转动一圈.图中OA与地面垂直.以OA为始边,逆时针转动θ角到OB,设B点与地面距离为h.

(1)求h与θ的函数解析式;
(2)设从OA开始转动,经过t秒到达OB,求h与t的函数解析式;
(3)填写下列表格:
θ | 0° | 30° | 60° | 90° | 120° | 150° | 180° |
h(m) |
|
|
|
|
|
|
|
t(s) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
h(m) |
|
|
|
|
|
|
|
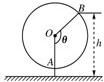 如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.
如图为一个缆车示意图,该缆车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动θ角到OB,设B点与地面距离是h.