题目内容
若二项式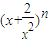 的展开式共7项,则n的值为 ,展开式中的常数项为 .
的展开式共7项,则n的值为 ,展开式中的常数项为 .
【答案】分析:由于二项式展开式中的展开项个数比二项式指数幂多一个,为此不难得出n为6,然后由通项公式Tr+1=Cnran-rbr求出通项并整理后可令x的指数幂为0,借此求出r的值后,即可计算常数项.
解答:解:因为展开式共有7项,所以二项式指数幂n=6,
设常数项为 =2rC6rx6-3r,令6-3r=0,
=2rC6rx6-3r,令6-3r=0,
∴r=2,所以常数项为22C62=60
所以答案分别填6和60
点评:本题主要考查二项式定理通项公式的应用,一般在求常数项时,解决办法是将通项中化简后的式子令x的指数幂为0来确定.这类问题通常属于属于基础题型.
解答:解:因为展开式共有7项,所以二项式指数幂n=6,
设常数项为
 =2rC6rx6-3r,令6-3r=0,
=2rC6rx6-3r,令6-3r=0,∴r=2,所以常数项为22C62=60
所以答案分别填6和60
点评:本题主要考查二项式定理通项公式的应用,一般在求常数项时,解决办法是将通项中化简后的式子令x的指数幂为0来确定.这类问题通常属于属于基础题型.

练习册系列答案
相关题目
 的展开式共7项,则n的值为 ,展开式中的常数项为 .
的展开式共7项,则n的值为 ,展开式中的常数项为 . 的展开式共7项,则n的值为 ,展开式中的常数项为 .
的展开式共7项,则n的值为 ,展开式中的常数项为 .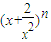 的展开式共7项,则n的值为 ,展开式中的常数项为 .
的展开式共7项,则n的值为 ,展开式中的常数项为 .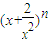 的展开式共7项,则n的值为 ,展开式中的常数项为 .
的展开式共7项,则n的值为 ,展开式中的常数项为 .