Question

10．已知点A（1，3），而且F₁是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的左焦点，P是椭圆上任意一点，求|PA|-|PF₁|的最小值．

Answer 1

分析 可先画出图形，根据椭圆的定义可得到|PA|-|PF₁|=|PA|+|PF₂|-6，从而只要求|PA|+|PF₂|的最小值便可得出|PA|-|PF₁|的最小值，而通过图形便可看出|PA|+|PF₂|的最小值为|AF₂|，这样即可求出|PA|-|PF₁|的最小值．

解答 解：如图，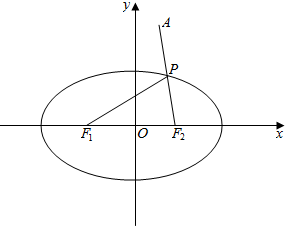

设椭圆的右焦点为F₂（2，0），根据椭圆的定义：
|PF₁|+|PF₂|=2a=6；
∴|PF₁|=6-|PF₂|；
∴|PA|-|PF₁|=|PA|-（6-|PF₂|）=|PA|+|PF₂|-6；
∴|PA|+|PF₂|最小时，|PA|-|PF₁|最小；
由图看出|PA|+|PF₂|的最小值为|AF₂|=$\sqrt{1+9}=\sqrt{10}$；
∴|PA|-|PF₁|的最小值为$\sqrt{10}-6$．

点评 考查椭圆的标准方程，椭圆的焦点，以及椭圆的定义，两边之和大于第三边定理．