题目内容
有向线段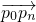 的n等分点从左到右依次为p1,p2,…pn-2,pn-1,记
的n等分点从左到右依次为p1,p2,…pn-2,pn-1,记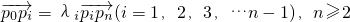 ,则λ1•λ2…λn-1=________.
,则λ1•λ2…λn-1=________.
1
分析:因为Pi是有向线段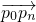 的第i个分点,可得
的第i个分点,可得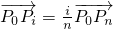 ,再根据
,再根据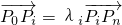 ,可得
,可得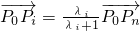 .所以
.所以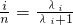 ,解之得λi=
,解之得λi=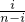 ,所以λ1•λ2…λn-1=
,所以λ1•λ2…λn-1=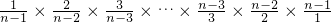 =1.
=1.
解答:∵Pi是有向线段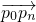 的第i个分点,∴
的第i个分点,∴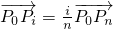 …①
…①
又∵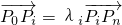 ,可得
,可得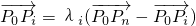
∴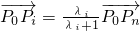 …②
…②
比较①②,可得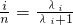 ,解之得λi=
,解之得λi=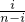 ,其中i=1、2、3、…、n-1
,其中i=1、2、3、…、n-1
∴λ1•λ2…λn-1=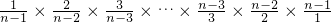 =1
=1
故答案为:1
点评:本题给出有向线段的几个等分点,在已知向量等式的情况下求参数的积,着重考查了平面向量基本定理及其应用,属于中档题.
分析:因为Pi是有向线段
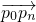 的第i个分点,可得
的第i个分点,可得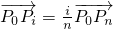 ,再根据
,再根据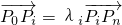 ,可得
,可得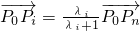 .所以
.所以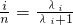 ,解之得λi=
,解之得λi=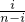 ,所以λ1•λ2…λn-1=
,所以λ1•λ2…λn-1=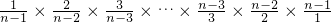 =1.
=1.解答:∵Pi是有向线段
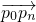 的第i个分点,∴
的第i个分点,∴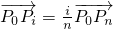 …①
…①又∵
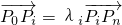 ,可得
,可得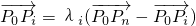
∴
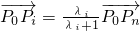 …②
…②比较①②,可得
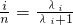 ,解之得λi=
,解之得λi=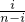 ,其中i=1、2、3、…、n-1
,其中i=1、2、3、…、n-1∴λ1•λ2…λn-1=
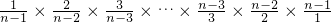 =1
=1故答案为:1
点评:本题给出有向线段的几个等分点,在已知向量等式的情况下求参数的积,着重考查了平面向量基本定理及其应用,属于中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
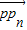 的n等分点从左到右依次为p1,p2,…pn-2,pn-1,记
的n等分点从左到右依次为p1,p2,…pn-2,pn-1,记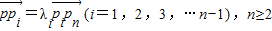 ,则λ1•λ2…λn-1= .
,则λ1•λ2…λn-1= .