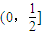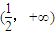题目内容
若函数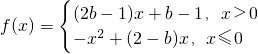
在R上为增函数，则实数b的取值范围为
- A.[1，2]
- B.
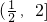
- C.（1，2]
- D.（1，2）
A
分析：要使f（x）在R上为增函数，须保证f（x）在（0，+∞），（-∞，0）上递增，且-02+（2-b）×0≤（2b-1）×0+b-1．
解答：令f1（x）=（2b-1）x+b-1（x＞0），f2（x）=-x2+（2-b）x（x≤0），
要使f（x）在R上为增函数，须有f1（x）递增，f2（x）递增，且f2（0）≤f1（0），
即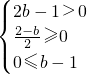
，解得1≤b≤2．
故选A．
点评：本题考查函数单调性的性质，应熟练数掌握形结合思想在分析问题中的应用．
分析：要使f（x）在R上为增函数，须保证f（x）在（0，+∞），（-∞，0）上递增，且-02+（2-b）×0≤（2b-1）×0+b-1．
解答：令f1（x）=（2b-1）x+b-1（x＞0），f2（x）=-x2+（2-b）x（x≤0），
要使f（x）在R上为增函数，须有f1（x）递增，f2（x）递增，且f2（0）≤f1（0），
即
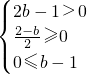，解得1≤b≤2．故选A．
点评：本题考查函数单调性的性质，应熟练数掌握形结合思想在分析问题中的应用．
练习册系列答案
相关题目
在R上为增函数，则a的取值范围是
)
在R上为增函数，则a的取值范围是 （ ） 
B．
C．
D．
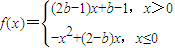在R上为增函数，则实数b的取值范围为（ ）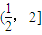
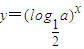在R上为增函数，则a的取值范围是（ ）
）
