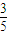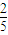题目内容
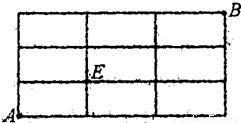
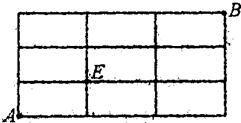 如图,棋盘式街道中,某人从A地出发到达B地.若限制行进的方向只能向右或向上,那么不经过E地的概率为( )
如图,棋盘式街道中,某人从A地出发到达B地.若限制行进的方向只能向右或向上,那么不经过E地的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由题意知本题是一个古典概型,试验发生包含的事件从A地出发到达B地,限制行进的方向只能向右或向上是6步走完,
选出6步中向右的3步C63剩下3步向上C33,经过E点,有A→右→上E,A→上→右E,两种情况,E到B点有C42种,做出经过E点的概率,根据对立事件的概率得到结果.
选出6步中向右的3步C63剩下3步向上C33,经过E点,有A→右→上E,A→上→右E,两种情况,E到B点有C42种,做出经过E点的概率,根据对立事件的概率得到结果.
解答:解:∵从A地出发到达B地,限制行进的方向只能向右或向上,
∴无论怎么走都是6步走完,
选出6步中向右的3步C63剩下3步向上C33,
∴一共有C63C33=20种走法,
经过E点,有A→右→上E,
A→上→右E,
E到B点,有C42=6种,
∴经过点E的有2×6=12种结果,
∴不经过E地的概率为1-
=
故选D.
∴无论怎么走都是6步走完,
选出6步中向右的3步C63剩下3步向上C33,
∴一共有C63C33=20种走法,
经过E点,有A→右→上E,
A→上→右E,
E到B点,有C42=6种,
∴经过点E的有2×6=12种结果,
∴不经过E地的概率为1-
| 12 |
| 20 |
| 2 |
| 5 |
故选D.
点评:本题主要考查古典概型,解决古典概型问题时最有效的工具是列举,要求能通过列举解决古典概型问题,也有一些题目需要借助于排列组合来计数.

练习册系列答案
相关题目

 B.
B. C.
C.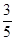 D.
D. 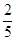

 B、
B、 C、
C、 D、
D、
 B、
B、 C、
C、 D、
D、