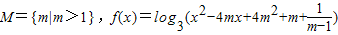题目内容
设m是常数,集合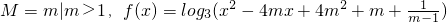
(1)证明:当m∈M时,f(x)对所有的实数x都有意义;
(2)当m∈M时,求函数f(x)的最小值;
(3)求证:对每个m∈M,函数f(x)的最小值都不于1.
解:(1)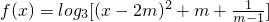 ,
,
当m∈M,即 m>1时,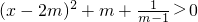 恒成立,
恒成立,
故f(x)的定义域为R.
(2)设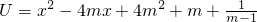 ,
,
∵y=log3U是增函数,
∴当U最小时f(x)最小.
而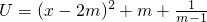 ,显然当x=2m时,U的最小值为
,显然当x=2m时,U的最小值为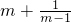 ,
,
此时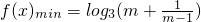 .
.
(3)m∈M时,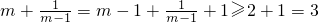 ,当且仅当m-1=1时,即m=2时,等号成立,
,当且仅当m-1=1时,即m=2时,等号成立,
所以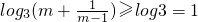 ,即函数f(x)的最小值都不小于1.
,即函数f(x)的最小值都不小于1.
分析:(1)化简函数的解析式为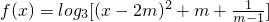 ,m>1时,
,m>1时,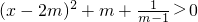 恒成立,故f(x)的定义域为R.
恒成立,故f(x)的定义域为R.
(2)设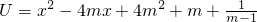 ,由于y=log3U是增函数,故当U最小f(x)最小,再由U的最小值为
,由于y=log3U是增函数,故当U最小f(x)最小,再由U的最小值为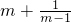 ,求得f(x)的最小值.
,求得f(x)的最小值.
(3)根据m∈M时,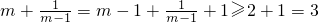 ,从而证得函数f(x)的最小值都不小于1.
,从而证得函数f(x)的最小值都不小于1.
点评:本题主要考查基本不等式在最值问题中的应用,对数函数的图象性质的应用,属于中档题.
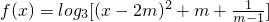 ,
,当m∈M,即 m>1时,
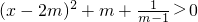 恒成立,
恒成立,故f(x)的定义域为R.
(2)设
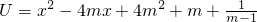 ,
,∵y=log3U是增函数,
∴当U最小时f(x)最小.
而
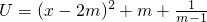 ,显然当x=2m时,U的最小值为
,显然当x=2m时,U的最小值为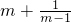 ,
,此时
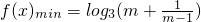 .
.(3)m∈M时,
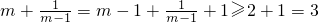 ,当且仅当m-1=1时,即m=2时,等号成立,
,当且仅当m-1=1时,即m=2时,等号成立,所以
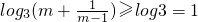 ,即函数f(x)的最小值都不小于1.
,即函数f(x)的最小值都不小于1.分析:(1)化简函数的解析式为
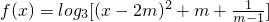 ,m>1时,
,m>1时,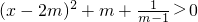 恒成立,故f(x)的定义域为R.
恒成立,故f(x)的定义域为R.(2)设
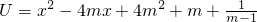 ,由于y=log3U是增函数,故当U最小f(x)最小,再由U的最小值为
,由于y=log3U是增函数,故当U最小f(x)最小,再由U的最小值为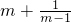 ,求得f(x)的最小值.
,求得f(x)的最小值.(3)根据m∈M时,
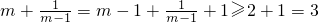 ,从而证得函数f(x)的最小值都不小于1.
,从而证得函数f(x)的最小值都不小于1.点评:本题主要考查基本不等式在最值问题中的应用,对数函数的图象性质的应用,属于中档题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目