题目内容
设y=3sin(x+φ)的图象为C,下列判断错误的是( )
A、过点(
| ||
B、过点(-
| ||
| C、C为长度为2π的闭区间上至多有两个最高点 | ||
| D、C在长度为π的闭区间上必有最高点和最低点 |
分析:首先根据y=3sin(x+φ)分别判断最大值最小值与周期,然后根据三角函数的性质判断选项.
解答:解:∵y=3sin(x+φ)
∴可以判断函数的最大值为3,最小值为-3,
周期为2π
则A、过点(
,3)的C唯一,因为此点为最高点,横坐标必唯一,正确
B、过点(-
,0)的C不唯一,因为此点为x轴上的点,根据φ的不同横坐标有所不同,故正确.
C、C为长度为2π的闭区间上至多有两个最高点.根据函数周期为2π,故正确
D、C在长度为π的闭区间上必有最高点和最低点,根据函数周期为2π,故错误.
故选D.
∴可以判断函数的最大值为3,最小值为-3,
周期为2π
则A、过点(
| π |
| 3 |
B、过点(-
| π |
| 6 |
C、C为长度为2π的闭区间上至多有两个最高点.根据函数周期为2π,故正确
D、C在长度为π的闭区间上必有最高点和最低点,根据函数周期为2π,故错误.
故选D.
点评:本题考查正弦函数的图象,通过对函数最值与周期性的分析对选项进行判断,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
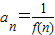 ,问数列是否存在最小项,若有求出此项,若无说明理由?
,问数列是否存在最小项,若有求出此项,若无说明理由? ,3)的C唯一
,3)的C唯一 ,0)的C不唯一
,0)的C不唯一