题目内容
设全集U=R,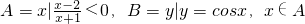 ,则A∩B=
,则A∩B=
- A.(cos2,1]
- B.[cos2,1]
- C.(-1,2)
- D.(-1,cos2]
A
分析:根据集合A中的不等式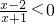 得到x-2与x+1异号,列出不等式求出解集即可得到集合A,再根据正弦函数的图象得到集合B,求出A与B的交集即可.
得到x-2与x+1异号,列出不等式求出解集即可得到集合A,再根据正弦函数的图象得到集合B,求出A与B的交集即可.
解答: 解:由
解:由 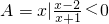 得到
得到 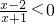 ,
,
即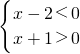 或
或 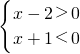 ,解得-1<x<2;
,解得-1<x<2;
根据正弦函数图象得到:cos2<y<1
所以A=(-1,2),B=(cos2,1)
∴A∩B=(cos2,1).
故选A
点评:此题要求学生会根据正弦函数的图象求值域,掌握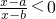 这种不等式的解法,以及会求两个集合的交集运算.属于基础题.
这种不等式的解法,以及会求两个集合的交集运算.属于基础题.
分析:根据集合A中的不等式
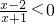 得到x-2与x+1异号,列出不等式求出解集即可得到集合A,再根据正弦函数的图象得到集合B,求出A与B的交集即可.
得到x-2与x+1异号,列出不等式求出解集即可得到集合A,再根据正弦函数的图象得到集合B,求出A与B的交集即可.解答:
 解:由
解:由 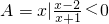 得到
得到 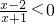 ,
,即
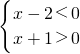 或
或 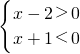 ,解得-1<x<2;
,解得-1<x<2;根据正弦函数图象得到:cos2<y<1
所以A=(-1,2),B=(cos2,1)
∴A∩B=(cos2,1).
故选A
点评:此题要求学生会根据正弦函数的图象求值域,掌握
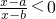 这种不等式的解法,以及会求两个集合的交集运算.属于基础题.
这种不等式的解法,以及会求两个集合的交集运算.属于基础题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则A∩B=( )
,则A∩B=( )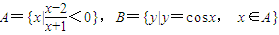 ,则A∩B=( )
,则A∩B=( )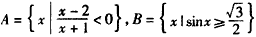 ,则A∩B=( )。
,则A∩B=( )。