题目内容
一袋中装有4个白球，2个红球，现从袋中往外取球，每次取出一个，取出后记下球的颜色，然后放回，直到红球出现3次停止，设停止时，取球次数为随机变量x，则P（x=5）=
．
| 8 |
| 81 |
| 8 |
| 81 |
分析：由题意知本题是一个独立重复试验，先算出从6个球中摸一个球，这个球是红色的概率是
，理解当x=5时，表示取球一共做了5次，且最后一次摸到红球，根据独立重复试验的公式得到结果．
| 1 |
| 3 |
解答：解：由题意知本题是一个独立重复试验，
从6个球中摸一个球，这个球是红色的概率是
，
取球次数为随机变量x，当x=5时，表示取球一共做了5次，且最后一次摸到红球，
∴P（x=5）=
(
)2(
)2×
=
，
故答案为：
．
从6个球中摸一个球，这个球是红色的概率是
| 1 |
| 3 |
取球次数为随机变量x，当x=5时，表示取球一共做了5次，且最后一次摸到红球，
∴P（x=5）=
| C | 2 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 81 |
故答案为：
| 8 |
| 81 |
点评：独立重复试验要从三方面考虑①每次试验是在同样条件下进行，②各次试验中的事件是相互独立的，③每次试验都只有两种结果，即事件要么发生，要么不发生，判断出符合试验，后面只要用公式就可以．
练习册系列答案
相关题目
___________.
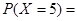