题目内容
过抛物线x2=4y上不同两点A、B分别作抛物线的切线相交于点P(x,y),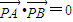 .
.(1)求y;
(2)求证:直线AB恒过定点;
(3)设(2)中直线AB恒过定点F,是否存在实数λ,使
 恒成立?若存在,求出λ的值,若不存在,请说明理由.
恒成立?若存在,求出λ的值,若不存在,请说明理由.
【答案】分析:(1)设A,B的坐标,求得直线PA、PB的方程,利用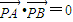 ,可得y;
,可得y;
(2)求出直线AB的方程,令x=0,结合(1)的结论,即可证得直线AB恒过定点;
(3)利用坐标表示向量,结合数量积公式,即可得到结论.
解答:(1)解:设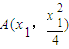 ,
, ,(x1≠x2).
,(x1≠x2).
由x2=4y,得: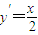 ,∴
,∴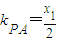 ,
,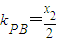
∵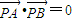 ,∴PA⊥PB,∴x1x2=-4.
,∴PA⊥PB,∴x1x2=-4.
直线PA的方程是: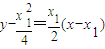 ,即
,即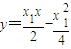 .①
.①
同理,直线PB的方程是: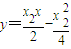 .②
.②
由①②得: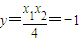 ,(x1,x2∈R).…(4分)
,(x1,x2∈R).…(4分)
(2)证明:由(1)可得直线AB的方程为
令x=0,可得 ,
,
∵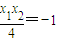 ,∴y=1
,∴y=1
∴直线AB恒过点(0,1)…(8分)
(3)解:由(1)得: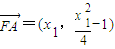 ,
,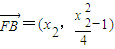 ,x1x2=-4,
,x1x2=-4,
∴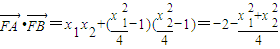
∵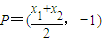 ,∴
,∴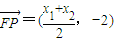 ,
,
∴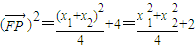 ,
,
∴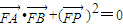 .
.
故存在λ=1使得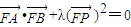 .…(12分)
.…(12分)
点评:本题考查直线与抛物线的位置关系,考查直线恒过定点,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
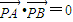 ,可得y;
,可得y;(2)求出直线AB的方程,令x=0,结合(1)的结论,即可证得直线AB恒过定点;
(3)利用坐标表示向量,结合数量积公式,即可得到结论.
解答:(1)解:设
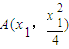 ,
, ,(x1≠x2).
,(x1≠x2).由x2=4y,得:
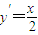 ,∴
,∴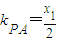 ,
,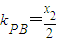
∵
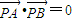 ,∴PA⊥PB,∴x1x2=-4.
,∴PA⊥PB,∴x1x2=-4.直线PA的方程是:
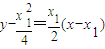 ,即
,即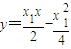 .①
.①同理,直线PB的方程是:
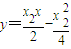 .②
.②由①②得:
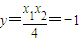 ,(x1,x2∈R).…(4分)
,(x1,x2∈R).…(4分)(2)证明:由(1)可得直线AB的方程为

令x=0,可得
 ,
,∵
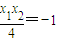 ,∴y=1
,∴y=1∴直线AB恒过点(0,1)…(8分)
(3)解:由(1)得:
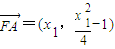 ,
,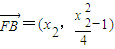 ,x1x2=-4,
,x1x2=-4,∴
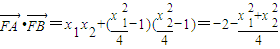
∵
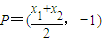 ,∴
,∴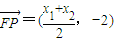 ,
,∴
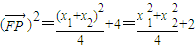 ,
,∴
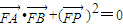 .
.故存在λ=1使得
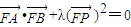 .…(12分)
.…(12分)点评:本题考查直线与抛物线的位置关系,考查直线恒过定点,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
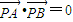 .
.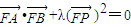 ?若存在,求出λ的值,若不存在,请说明理由.
?若存在,求出λ的值,若不存在,请说明理由.