题目内容
在极坐标系中,圆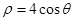 上的点到直线
上的点到直线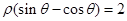 的最大距离为 .
的最大距离为 .
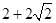
解析试题分析:将圆的极坐标方程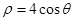 化为普通方程为
化为普通方程为 ,同时将直线的极坐标方程
,同时将直线的极坐标方程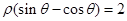 也化为普通方程为
也化为普通方程为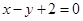 ,计算圆心
,计算圆心 到直线的距离
到直线的距离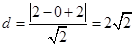 ,有
,有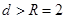 ,说明直线与圆相离,所以圆上的点到直线的最大距离为
,说明直线与圆相离,所以圆上的点到直线的最大距离为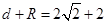 .
.
考点:1.极坐标方程与普通方程的互化;2.直线与圆的位置关系.

练习册系列答案
相关题目
若直线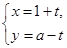 (
(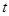 为参数)被圆
为参数)被圆 (
(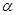 为参数)所截的弦长为
为参数)所截的弦长为 ,则
,则 的值为( )
的值为( )
A.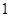 或 或 | B.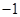 或 或 |
C.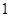 或 或 | D.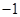 或 或 |
极坐标方程( —1)(
—1)(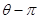 )=0(
)=0(
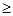 0)表示的图形是 ( )
0)表示的图形是 ( )
| A.两个圆 | B.两条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
极坐标方程(p-1)( )=(p
)=(p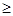 0)表示的图形是( )
0)表示的图形是( )
| A.两个圆 | B.两条直线 |
| C.一个圆和一条射线 | D.一条直线和一条射线 |
设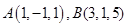 ,则线段AB的中点在空间直角坐标系中的位置是 ( )
,则线段AB的中点在空间直角坐标系中的位置是 ( )
A.在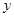 轴上 轴上 | B.在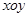 面内 面内 | C.在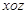 面内 面内 | D.在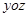 面内 面内 |
 (
( 为参数)的焦点坐标是
为参数)的焦点坐标是 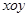 中,圆C的参数方程为
中,圆C的参数方程为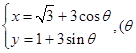 为参数),以
为参数),以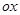 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线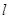 的极坐标方程为
的极坐标方程为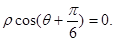 则直线
则直线 的圆心C到直线
的圆心C到直线 的距离为____
的距离为____ 的圆心到直线
的圆心到直线 的距离是_______________.
的距离是_______________.