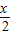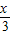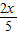题目内容
已知P={x|0≤x≤4},Q={y|0≤y≤2},下列不表示从P到Q的映射的是①f:x→y=
| x |
| 2 |
②f:x→y=
| x |
| 3 |
③f:x→y=
| 3x |
| 2 |
④f:x→y=
| 2x |
| 5 |
分析:本题根据映射的概念逐一判断:
由x∈[0,4]可求出y的范围,然后判断其与集合Q的关系,
①y=
∈[0,2]⊆Q,②y=
∈[0,
]⊆Q,③y=
∈[0,6]?Q,④y=
∈[0,
]⊆Q.
于是否是从P到Q的映射应经可以判断.
由x∈[0,4]可求出y的范围,然后判断其与集合Q的关系,
①y=
| x |
| 2 |
| x |
| 3 |
| 4 |
| 3 |
| 3x |
| 2 |
| 2x |
| 5 |
| 8 |
| 5 |
于是否是从P到Q的映射应经可以判断.
解答:解:本题根据映射的概念逐一判断:
由x∈[0,4]知:
①y=
∈[0,2]⊆Q,所以此对应f是从P到Q的映射
②y=
∈[0,
]⊆Q,所以此对应f是从P到Q的映射
③y=
∈[0,6]?Q,所以此对应f不是从P到Q的映射
④y=
∈[0,
]⊆Q,所以此对应f是从P到Q的映射
故答案为:③
由x∈[0,4]知:
①y=
| x |
| 2 |
②y=
| x |
| 3 |
| 4 |
| 3 |
③y=
| 3x |
| 2 |
④y=
| 2x |
| 5 |
| 8 |
| 5 |
故答案为:③
点评:本题考查了映射的概念.判断一个对应是否是一个映射的方法.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知P={x|0≤x≤5},Q={y|0≤y≤3},下列不表示从P到Q的函数的是( )
A、f:x→y=
| ||
B、f:x→y=
| ||
C、f:x→y=
| ||
D、f:x→y=
|
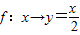
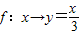
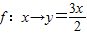
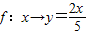 .
.