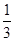题目内容
袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球.从袋中任取两球,两球颜色不同的概率为( )
A. | B. | C.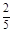 | D. |
D
解析试题分析:令红球、白球、黑球分别为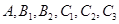 ,则从袋中任取两球有
,则从袋中任取两球有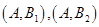 ,
,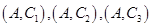 ,
,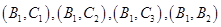 ,
,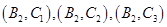 ,
,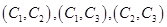 共15种取法,其中两球颜色相同有
共15种取法,其中两球颜色相同有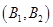 ,
,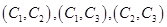 共4种取法,由古典概型及对立事件的概率公式可得
共4种取法,由古典概型及对立事件的概率公式可得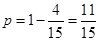 .
.
考点:古典概型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知 ,若
,若 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,其中
,其中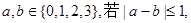 则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )
A.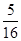 | B.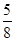 | C.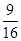 | D.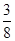 |
下列叙述随机事件的频率与概率的关系中,说法正确的是( )
| A.频率就是概率 |
| B.频率是客观存在的,与试验次数无关 |
| C.随着试验次数的增多,频率越来越接近概率 |
| D.概率是随机的,在试验前不能确定 |
已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X>4)=( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.15858 |




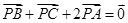 ,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )
,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是( )