题目内容
 设全集U=R集合M={x|x2-x≤0},N={x|y=lg
设全集U=R集合M={x|x2-x≤0},N={x|y=lg| 2x-1 |
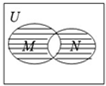
分析:图中阴影部分所表示的范围是[(CUM)∩N]∪[(CUN)∩M],由全集U=R,集合M={x|x2-x≤0}={x|0≤x≤1},N={x|y=lg
}={x|
}={x|x>
},先分别求出CUM和CUN,由此能求出图中阴影部分所表示的范围.
| 2x-1 |
|
| 1 |
| 2 |
解答:解:图中阴影部分所表示的范围是[(CUM)∩N]∪[(CUN)∩M],
∵全集U=R,集合M={x|x2-x≤0}={x|0≤x≤1},
N={x|y=lg
}={x|
}={x|x>
},
∴CUM={x|x<0,或x>1},CUN={x|x≤
},
∴[(CUM)∩N]∪[(CUN)∩M]=(1,+∞)∪[0,
],
故选C.
∵全集U=R,集合M={x|x2-x≤0}={x|0≤x≤1},
N={x|y=lg
| 2x-1 |
|
| 1 |
| 2 |
∴CUM={x|x<0,或x>1},CUN={x|x≤
| 1 |
| 2 |
∴[(CUM)∩N]∪[(CUN)∩M]=(1,+∞)∪[0,
| 1 |
| 2 |
故选C.
点评:本题考查文氏图表示集合的运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
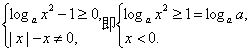 ,a>1},则
,a>1},则