题目内容
一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).(1)过此棱锥的高以及一底边中点F作棱锥的截面(如图),设截面三角形面积为y,求y的最大值及y取最大值时的x的值;
(2)空间一动点P满足
 (a+b+c=1),在第(1)问的条件下,求
(a+b+c=1),在第(1)问的条件下,求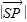 的最小值,并求取得最小值时a,b,c的值;
的最小值,并求取得最小值时a,b,c的值;(3)在第(1)问的条件下,设F是CD的中点,问是否存在这样的动点Q,它在此棱锥的表面(包含底面ABCD)运动,且FQ⊥AC?如果存在,计算其运动轨迹的长度,如果不存在,说明理由.

【答案】分析:(1)在直角三角形中根据两条边长利用勾股定理做出四棱锥的高,即可求得截面三角形面积的函数表达式;
(2)先证明P,A,B,C共面,即P∈平面ABC,从而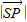 的最小值即是S到平面ABC的距离SO;
的最小值即是S到平面ABC的距离SO;
(3)取BC的中点G,SC中点T,连接FG,GT,TF,证明AC⊥平面GFT即可得到结论,从而可求轨迹的长度.
解答:解:(1)由题意,y= EF•SO=
EF•SO=
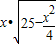 =
=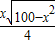 (0<x<10)….(2分)
(0<x<10)….(2分)
∴y=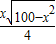 =
=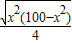 ≤
≤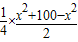 =
=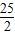 .
.
当且仅当x2=100-x2,即x=5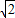 时取得最大值.…..(4分)
时取得最大值.…..(4分)
(2)由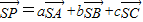 (a+b+c=1),得
(a+b+c=1),得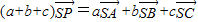 ,
,
∴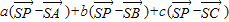 =
=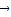 ,
,
∴a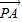 =-b
=-b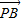 -c
-c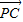 ,
,
∴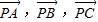 共面,
共面,
∴P,A,B,C共面,即P∈平面ABC.
∴ 的最小值即是S到平面ABC的距离SO,
的最小值即是S到平面ABC的距离SO,
在上问条件下,SO=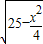 =
=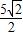 …(7分)
…(7分)
此时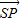 =
=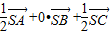 ,即a=
,即a= ,b=0,c=
,b=0,c= …(9分)
…(9分)
(3)存在这样的点的轨迹,下面证明:
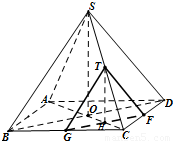
取BC的中点G,SC中点T,连接FG,GT,TF,FG∩AC=H,则GF∥BD,TH∥SO
∵SO⊥AC,BD⊥AC
∴AC⊥GF,AC⊥TH
∵GF∩TH=H
∴AC⊥平面GFT.
∴只要Q在平面GFT与棱锥的表面的交线上运动,均有FQ⊥AC.
此时,由中位线性质可知,△GFT的周长l= (SB+BD+SD)=
(SB+BD+SD)=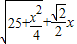 ,
,
在(1)的条件下,l=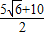 …..(14分)
…..(14分)
点评:本题考查函数模型的构建,考查向量知识的运用,考查线面垂直,考查学生分析解决问题的能力,属于中档题.
(2)先证明P,A,B,C共面,即P∈平面ABC,从而
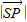 的最小值即是S到平面ABC的距离SO;
的最小值即是S到平面ABC的距离SO;(3)取BC的中点G,SC中点T,连接FG,GT,TF,证明AC⊥平面GFT即可得到结论,从而可求轨迹的长度.
解答:解:(1)由题意,y=
 EF•SO=
EF•SO=
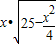 =
=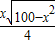 (0<x<10)….(2分)
(0<x<10)….(2分)∴y=
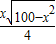 =
=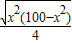 ≤
≤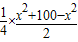 =
=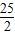 .
.当且仅当x2=100-x2,即x=5
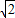 时取得最大值.…..(4分)
时取得最大值.…..(4分)(2)由
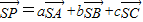 (a+b+c=1),得
(a+b+c=1),得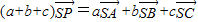 ,
,∴
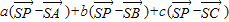 =
=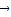 ,
,∴a
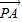 =-b
=-b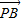 -c
-c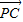 ,
,∴
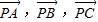 共面,
共面,∴P,A,B,C共面,即P∈平面ABC.
∴
 的最小值即是S到平面ABC的距离SO,
的最小值即是S到平面ABC的距离SO,在上问条件下,SO=
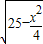 =
=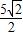 …(7分)
…(7分)此时
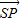 =
=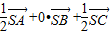 ,即a=
,即a= ,b=0,c=
,b=0,c= …(9分)
…(9分)(3)存在这样的点的轨迹,下面证明:

取BC的中点G,SC中点T,连接FG,GT,TF,FG∩AC=H,则GF∥BD,TH∥SO
∵SO⊥AC,BD⊥AC
∴AC⊥GF,AC⊥TH
∵GF∩TH=H
∴AC⊥平面GFT.
∴只要Q在平面GFT与棱锥的表面的交线上运动,均有FQ⊥AC.
此时,由中位线性质可知,△GFT的周长l=
 (SB+BD+SD)=
(SB+BD+SD)=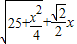 ,
,在(1)的条件下,l=
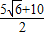 …..(14分)
…..(14分)点评:本题考查函数模型的构建,考查向量知识的运用,考查线面垂直,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

 一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥).
一块边长为10的正方形纸片,按如图所示将阴影部分裁下,然后将余下的四个全等的等腰三角形作为侧面制作一个正四棱锥S-ABCD(底面是正方形,顶点在底面的射影是底面中心的四棱锥). 一块边长为10
一块边长为10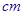 的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积
的正方形铁片按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试建立容器的容积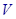 与
与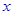 的函数关系式,并求出函数的定义域.
的函数关系式,并求出函数的定义域. 