Question

已知方程sinx+cosx=k在0≤x≤π上有两解，求k的取值范围．

Answer 1

分析：将方程sinx+cosx=k在0≤x≤π上有两解转化为两个简单函数y₁=

2

sin（x+

π

4

）与y₂=k的图象有两个交点的问题，即可得到答案．

解答：解：原方程sinx+cosx=k?

2

sin（x+

π

4

）=k，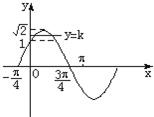
在同一坐标系内作函数y₁=

2

sin（x+

π

4

）与y₂=k的图象．
对于y=

2

sin（x+

π

4

），令x=0，得y=1．
∴当k∈[1，

2

）时，观察知两曲线在[0，π]上有两交点，方程有两解．

点评：本题是通过函数图象交点个数判断方程实数解的个数，应重视这种方法．