题目内容
若向量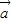 与
与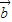 不共线,且|
不共线,且|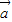 |=4,|
|=4,|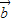 |=3.
|=3.(Ⅰ)k为何值时,向量
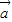 +k
+k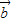 与
与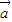 -k
-k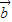 互相垂直;
互相垂直;(Ⅱ)若(2
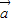 -3
-3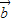 )(2
)(2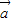 +
+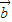 )=61,求
)=61,求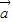 与
与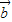 的夹角θ.
的夹角θ.
【答案】分析:(Ⅰ) +k
+k 与
与 -k
-k 垂直时,(
垂直时,(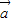 +k
+k )•(
)•( -k
-k )=0,利用数量积运算即可解得k值;
)=0,利用数量积运算即可解得k值;
(Ⅱ)利用数量积的运算性质及数量积及数量积定义化简等式可求得答案;
解答:解:(Ⅰ)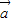 +k
+k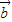 与
与 -k
-k 垂直时,(
垂直时,( +k
+k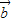 )•(
)•(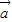 -k
-k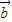 )=0,
)=0,
所以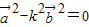 ,即16-9k2=0,解得k=
,即16-9k2=0,解得k= ,
,
所以当k= 时,向量
时,向量 +k
+k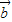 与
与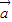 -k
-k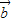 互相垂直;
互相垂直;
(Ⅱ)(2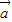 -3
-3 )•(2
)•(2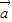 +
+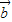 )=61,即
)=61,即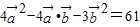 ,
,
所以4×42-4×4×3cosθ-3×32=61,解得cosθ=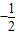 ,
,
所以 与
与 的夹角θ为120°.
的夹角θ为120°.
点评:本题考查平面向量数量积的运算、数量积表示两个向量的夹角,属中档题.
 +k
+k 与
与 -k
-k 垂直时,(
垂直时,(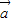 +k
+k )•(
)•( -k
-k )=0,利用数量积运算即可解得k值;
)=0,利用数量积运算即可解得k值;(Ⅱ)利用数量积的运算性质及数量积及数量积定义化简等式可求得答案;
解答:解:(Ⅰ)
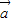 +k
+k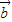 与
与 -k
-k 垂直时,(
垂直时,( +k
+k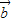 )•(
)•(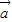 -k
-k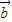 )=0,
)=0,所以
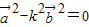 ,即16-9k2=0,解得k=
,即16-9k2=0,解得k= ,
,所以当k=
 时,向量
时,向量 +k
+k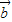 与
与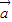 -k
-k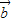 互相垂直;
互相垂直;(Ⅱ)(2
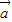 -3
-3 )•(2
)•(2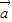 +
+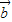 )=61,即
)=61,即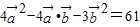 ,
,所以4×42-4×4×3cosθ-3×32=61,解得cosθ=
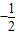 ,
,所以
 与
与 的夹角θ为120°.
的夹角θ为120°.点评:本题考查平面向量数量积的运算、数量积表示两个向量的夹角,属中档题.

练习册系列答案
相关题目
 与
与 不共线,
不共线,  =
= )
) 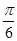 C.
C.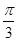 D.
D.
 与
与 不共线,
不共线,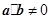 ,且
,且 ,则向量
,则向量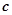 的夹角为( )
的夹角为( )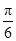 C.
C. D.
D.