题目内容
(本题满分12分)已知O(0,0)、A(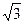 ,0)为平面内两定点,动点P满足|PO|+|PA|=2.
,0)为平面内两定点,动点P满足|PO|+|PA|=2.
(I)求动点P的轨迹方程;
(II)设直线 与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
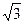 ,0)为平面内两定点,动点P满足|PO|+|PA|=2.
,0)为平面内两定点,动点P满足|PO|+|PA|=2.(I)求动点P的轨迹方程;
(II)设直线
 与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时
与(I)中点P的轨迹交于B、C两点.求△ABC的最大面积及此时(1)

(2)

(1)解:∵|PO|+|PA|=2,且|OA|=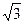 <2.
<2.
∴点P的轨迹是以O(0,0)、A( )为焦点,
)为焦点,
长轴长2a=2的椭圆.…………3分
∴a=1, 设P(x,y),
设P(x,y),
∴点P的轨迹方程为 …………5分
…………5分
(2)解:将y=kx代入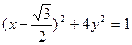 ,
,
消去x,整理为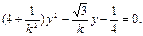 …………7分
…………7分
设 ,
,
则 …………8分
…………8分
= …………11分
…………11分
当且仅当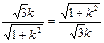 ,解得
,解得 时,△ABC的最大面积为
时,△ABC的最大面积为
此时直线l的方程是 …………13分
…………13分
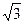 <2.
<2.∴点P的轨迹是以O(0,0)、A(
 )为焦点,
)为焦点,长轴长2a=2的椭圆.…………3分
∴a=1,
 设P(x,y),
设P(x,y),∴点P的轨迹方程为
 …………5分
…………5分(2)解:将y=kx代入
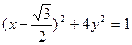 ,
,消去x,整理为
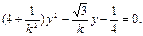 …………7分
…………7分设
 ,
,则
 …………8分
…………8分=
 …………11分
…………11分当且仅当
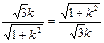 ,解得
,解得 时,△ABC的最大面积为
时,△ABC的最大面积为
此时直线l的方程是
 …………13分
…………13分
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 且
且 ,求:
,求: 的最小值;
的最小值;  与
与 轴、
轴、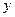 轴分别交于
轴分别交于 、
、 ,求
,求 (O为坐标原点)面积的最小值.
(O为坐标原点)面积的最小值. 两条直线
两条直线 ,
,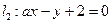 ,若
,若 ,则
,则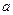 =___ ____.
=___ ____.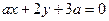 与直线
与直线 平行,则实数
平行,则实数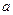 的值为
的值为  0射向直线l: y=x被直线反射后的光线所在的方程是 ( )
0射向直线l: y=x被直线反射后的光线所在的方程是 ( ) D 2x-y+3=0.
D 2x-y+3=0. 平行的直线方程是 ( )
平行的直线方程是 ( )




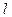 通过点(1,3)且与两坐标轴的正半轴所围成的三角形面积为6,则直线
通过点(1,3)且与两坐标轴的正半轴所围成的三角形面积为6,则直线


