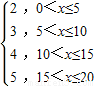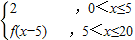题目内容
某市“招手即停”公共汽车的票价按下列规则制定:5公里以内(含5公里),票价2元;5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,根据题意,三位同学用了三种方式表示出的票价y=f(x)与里程x之间的关系分别如下:
(1)y=f(x)=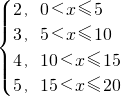
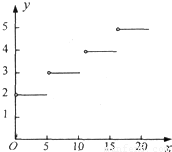
(2)
(3)f(x)=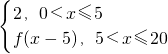
其中能正确反映出两者的函数关系有
- A.0个
- B.1个
- C.2个
- D.3个
C
分析:根据该规则可求出f(x)的解析式,可验证(1)正确;(2)为该函数的图象表示,故(2)正确;对于(3)可通过特值检验,说明其错误;
解答:由于5公里以内(含5公里),票价2元,所以当0<x≤5时f(x)=2;
由于5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算),且该线路里程为20公里,
所以5<x≤10时f(x)=3;当10<x≤15时f(x)=4,15<x≤20时f(x)=5;
故f(x)= ,(1)正确;
,(1)正确;
(2)为该分段函数f(x)的图象,(2)正确;
由该规则知f(6)=2+1=3,而(3)中,f(6)=f(6-5)=f(1)=2,矛盾,故(3)错误;
所以能正确反映出两者的函数关系有2个,
故选C.
点评:本题考查分段函数解析式的求法及其图象,考查分类讨论思想,考查学生解决实际问题的能力.
分析:根据该规则可求出f(x)的解析式,可验证(1)正确;(2)为该函数的图象表示,故(2)正确;对于(3)可通过特值检验,说明其错误;
解答:由于5公里以内(含5公里),票价2元,所以当0<x≤5时f(x)=2;
由于5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算),且该线路里程为20公里,
所以5<x≤10时f(x)=3;当10<x≤15时f(x)=4,15<x≤20时f(x)=5;
故f(x)=
 ,(1)正确;
,(1)正确;(2)为该分段函数f(x)的图象,(2)正确;
由该规则知f(6)=2+1=3,而(3)中,f(6)=f(6-5)=f(1)=2,矛盾,故(3)错误;
所以能正确反映出两者的函数关系有2个,
故选C.
点评:本题考查分段函数解析式的求法及其图象,考查分类讨论思想,考查学生解决实际问题的能力.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目