题目内容
设{an}是由正数组成的等比数列,公比q=2,且a1·a2·a3·…·a30=230,那么a3·a6·a9·…·a30等于( )
| A.210 | B.220 | C.216 | D.215 |
B
解析试题分析:由等比数列的定义,a1 ·a2 ·a3 =(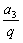 )3 ,故a1 ·a2 ·a3 ·…·a30 =(
)3 ,故a1 ·a2 ·a3 ·…·a30 =( )3 .又q=2,故a3 ·a6 ·a9 ·…·a30 =220,故选B
)3 .又q=2,故a3 ·a6 ·a9 ·…·a30 =220,故选B
考点:等比数列,
点评:主要是考查了等比数列的通项公式的运用,求解数列的积,属于基础题。

练习册系列答案
相关题目
下列数列为等比数列的是( )
| A.1,2,3,4,5,6, | B.1,2,4,8,16,32, |
| C.0,0,0,0,0,0, | D.1,-2,3,-4,5,-6, |
在等比数列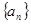 中,已知
中,已知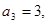
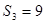 ,则
,则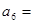 ( )
( )
A.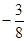 | B.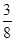 | C.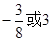 | D.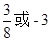 |
在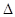 ABC中,
ABC中,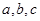 为
为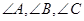 的对边,且
的对边,且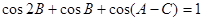 ,则( )
,则( )
A.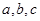 成等差数列 成等差数列 | B.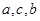 成等差数列 成等差数列 |
C.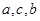 成等比数列 成等比数列 | D.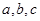 成等比数列 成等比数列 |
等比数列{ }中,若
}中,若 ,则
,则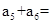 ( )
( )
| A.2 | B.40 | C.80 | D.120 |
已知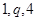 成等比数列,则
成等比数列,则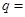 ( )
( )
A.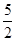 | B.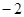 | C.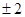 | D.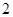 |
在等比数列{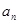 }中,若
}中,若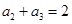 ,
,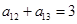 ,则
,则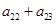 的值是( )
的值是( )
A.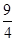 | B.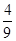 | C.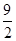 | D.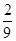 |
已知等比数列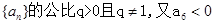 ,则 ( )
,则 ( )
A.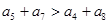 | B.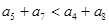 |
C.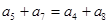 | D.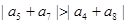 |
设 为等比数列
为等比数列 的前
的前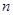 项和,已知
项和,已知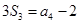 ,
,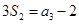 ,则公比
,则公比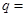 ( )
( )
| A.3 | B.4 | C.5 | D.6 |