题目内容
已知向量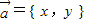 ,其中x∈{1,2,4,5},y∈{2,4,6,8},则满足条件的不共线的向量共有 个.
,其中x∈{1,2,4,5},y∈{2,4,6,8},则满足条件的不共线的向量共有 个.
【答案】分析:先根据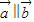 ⇒x1y2-x2y1=0,知道不共线向量,只需要x1y2-x2y1≠0;再对x的取值分四种情况讨论即可得出结论.
⇒x1y2-x2y1=0,知道不共线向量,只需要x1y2-x2y1≠0;再对x的取值分四种情况讨论即可得出结论.
解答:解:因为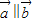 ⇒x1y2-x2y1=0.
⇒x1y2-x2y1=0.
所以要找不共线向量,只需要x1y2-x2y1≠0即可.
当x=1时,y=2,4,6,8符合要求
当x=2时,y=2,6符合要求
当x=5 时,y=2,4,6,8符合要求
当x=4时,y=2,6符合要求;
故满足要求的不共线向量共有4+2+4+2=12个.
故答案为:12.
点评:本题主要考查向量共线定理的应用.如果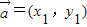 ,
,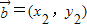 则,
则,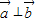 ⇒x1x2+y1y2=0;
⇒x1x2+y1y2=0;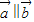 ⇒x1y2-x2y1=0.
⇒x1y2-x2y1=0.
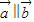 ⇒x1y2-x2y1=0,知道不共线向量,只需要x1y2-x2y1≠0;再对x的取值分四种情况讨论即可得出结论.
⇒x1y2-x2y1=0,知道不共线向量,只需要x1y2-x2y1≠0;再对x的取值分四种情况讨论即可得出结论.解答:解:因为
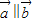 ⇒x1y2-x2y1=0.
⇒x1y2-x2y1=0.所以要找不共线向量,只需要x1y2-x2y1≠0即可.
当x=1时,y=2,4,6,8符合要求
当x=2时,y=2,6符合要求
当x=5 时,y=2,4,6,8符合要求
当x=4时,y=2,6符合要求;
故满足要求的不共线向量共有4+2+4+2=12个.
故答案为:12.
点评:本题主要考查向量共线定理的应用.如果
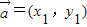 ,
,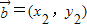 则,
则,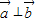 ⇒x1x2+y1y2=0;
⇒x1x2+y1y2=0;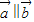 ⇒x1y2-x2y1=0.
⇒x1y2-x2y1=0. 
练习册系列答案
相关题目
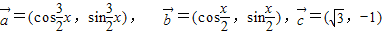 ,其中x∈R,
,其中x∈R,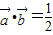 时,求x值的集合;
时,求x值的集合;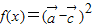 ,求f(x)的最小正周期及其单调增区间.
,求f(x)的最小正周期及其单调增区间.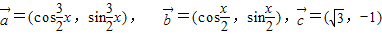 ,其中x∈R,
,其中x∈R,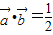 时,求x值的集合;
时,求x值的集合;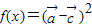 ,求f(x)的最小正周期及其单调增区间.
,求f(x)的最小正周期及其单调增区间.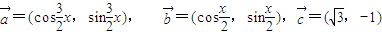 ,其中x∈R,
,其中x∈R,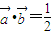 时,求x值的集合;
时,求x值的集合;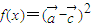 ,求f(x)的最小正周期及其单调增区间.
,求f(x)的最小正周期及其单调增区间.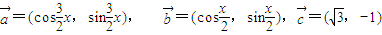 ,其中x∈R,
,其中x∈R,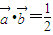 时,求x值的集合;
时,求x值的集合;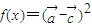 ,求f(x)的最小正周期及其单调增区间.
,求f(x)的最小正周期及其单调增区间. ,其中x>0.若
,其中x>0.若 ,则x的值为( )
,则x的值为( )