题目内容
已知函数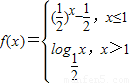 ,若f(a2-3)>f(2a),则实数a的取值范围是( )
,若f(a2-3)>f(2a),则实数a的取值范围是( )A.(-∞,-3)∪(-1,+∞)
B.(-∞,-1)∪(3,+∞)
C.(-3,1)
D.(-1,3)
【答案】分析:当x≤1时,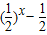 是减函数,又 当 x>1 时,
是减函数,又 当 x>1 时,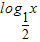 也是减函数,所以函数f(x)在R上是减函数,故由条件可得a2 -3<2a,由此解得a的范围.
也是减函数,所以函数f(x)在R上是减函数,故由条件可得a2 -3<2a,由此解得a的范围.
解答:解:当x≤1时, 是减函数,此时的最小值
是减函数,此时的最小值 =0.
=0.
又 当 x>1 时, 也是减函数,
也是减函数,
且当x=1时,两个端点的函数值分别为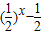 =0,及
=0,及  =0,
=0,
所以函数f(x)在R上是减函数.
因为f(a2-3)>f(2a),所以a2 -3<2a,即 a2 -2a-3<0,
解得3>a>-1.
故选 D.
点评:本题考查函数解析式的求解和常用方法,解题时要认真审题,注意分段函数的性质和应用,属于中档题.
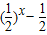 是减函数,又 当 x>1 时,
是减函数,又 当 x>1 时,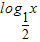 也是减函数,所以函数f(x)在R上是减函数,故由条件可得a2 -3<2a,由此解得a的范围.
也是减函数,所以函数f(x)在R上是减函数,故由条件可得a2 -3<2a,由此解得a的范围.解答:解:当x≤1时,
 是减函数,此时的最小值
是减函数,此时的最小值 =0.
=0.又 当 x>1 时,
 也是减函数,
也是减函数,且当x=1时,两个端点的函数值分别为
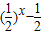 =0,及
=0,及  =0,
=0,所以函数f(x)在R上是减函数.
因为f(a2-3)>f(2a),所以a2 -3<2a,即 a2 -2a-3<0,
解得3>a>-1.
故选 D.
点评:本题考查函数解析式的求解和常用方法,解题时要认真审题,注意分段函数的性质和应用,属于中档题.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 ,若f(6-a2)>f(a)则实数a的取值范围是( )
,若f(6-a2)>f(a)则实数a的取值范围是( ) ,若f(6-a2)>f(5a),则实数a的取值范围是 .
,若f(6-a2)>f(5a),则实数a的取值范围是 .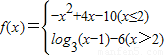 ,若f(6-a2)>f(5a),则实数a的取值范围是 .
,若f(6-a2)>f(5a),则实数a的取值范围是 . ,若f(2-a2)>f(a),则实数a的取值范围是( )。
,若f(2-a2)>f(a),则实数a的取值范围是( )。