题目内容
双曲线C的方程为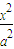 -
-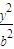 =1(a>0,b>0),l1,l2为其渐近线,F为右焦点,过F作l∥l2且l交双曲线C于R,交l1于M.若
=1(a>0,b>0),l1,l2为其渐近线,F为右焦点,过F作l∥l2且l交双曲线C于R,交l1于M.若 =λ
=λ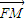 ,且λ∈(
,且λ∈( ,
, ),则双曲线的离心率的取值范围为( )
),则双曲线的离心率的取值范围为( )A.(1,
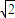 ]
]B.(
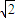 ,
,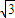 )
)C.(
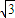 ,
,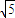 )
)D.(
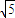 ,+∞)
,+∞)
【答案】分析:由题意,可给出渐近线的方程,直线l的方程,由题设条件建立方程解出两点M,R的坐标,从而给出两向量 ,
, 的坐标,代入
的坐标,代入 =λ
=λ ,由向量相等的得到关于a,c的方程,结合离心率的定义,将此方程转化为关于e的方程,解方程求出e即可选正确选项
,由向量相等的得到关于a,c的方程,结合离心率的定义,将此方程转化为关于e的方程,解方程求出e即可选正确选项
解答:解:由题意得l1:y=- ,l2:y=
,l2:y= ,l:y=
,l:y= ,
,
由l交双曲线C于R,令 ,解此方程组得R(
,解此方程组得R( )
)
故有 =(
=( )
)
由l交l1于M,令 解此方程组得M(
解此方程组得M( )
)
故有 =(-
=(- )
)
由 =λ
=λ ,得(
,得( )=λ(-
)=λ(- )
)
所以 ,整理得a2=(1-λ)c2,即e2=
,整理得a2=(1-λ)c2,即e2=
又λ∈( ,
, ),
),
∴e2∈(2,3),即e∈( ,
, )
)
故选B
点评:本题考查直线与直线,直线与双曲线交点的求法,离心率公式,向量的相等及向量坐标表示等知识,解题的关键是联立方程解出两交点的坐标,得到关于e的方程,本题计算量大,极易出错,但解题思维难度低,这是圆锥曲线问题的特点,做题时要严谨,避免计算失误造成解题无法进行,本题考查了计算能力,推理判断的能力及方程的思想转化的思想,属于计算难度较大的题
 ,
, 的坐标,代入
的坐标,代入 =λ
=λ ,由向量相等的得到关于a,c的方程,结合离心率的定义,将此方程转化为关于e的方程,解方程求出e即可选正确选项
,由向量相等的得到关于a,c的方程,结合离心率的定义,将此方程转化为关于e的方程,解方程求出e即可选正确选项解答:解:由题意得l1:y=-
 ,l2:y=
,l2:y= ,l:y=
,l:y= ,
,由l交双曲线C于R,令
 ,解此方程组得R(
,解此方程组得R( )
)故有
 =(
=( )
)由l交l1于M,令
 解此方程组得M(
解此方程组得M( )
)故有
 =(-
=(- )
)由
 =λ
=λ ,得(
,得( )=λ(-
)=λ(- )
)所以
 ,整理得a2=(1-λ)c2,即e2=
,整理得a2=(1-λ)c2,即e2=
又λ∈(
 ,
, ),
),∴e2∈(2,3),即e∈(
 ,
, )
)故选B
点评:本题考查直线与直线,直线与双曲线交点的求法,离心率公式,向量的相等及向量坐标表示等知识,解题的关键是联立方程解出两交点的坐标,得到关于e的方程,本题计算量大,极易出错,但解题思维难度低,这是圆锥曲线问题的特点,做题时要严谨,避免计算失误造成解题无法进行,本题考查了计算能力,推理判断的能力及方程的思想转化的思想,属于计算难度较大的题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“双曲线C的一条渐近线方程为4x-3y=0”是“双曲线C的方程为
-
=1”的( )
| x2 |
| 9 |
| y2 |
| 16 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、不充分不必要条件 |