题目内容
(本小题满分14分)已知函数 ,
, ,
,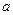 为常数.
为常数.
(1) 求函数 的定义域
的定义域 ;
;
(2) 若 时,对于
时,对于 ,比较
,比较 与
与 的大小;
的大小;
(3) 讨论方程 解的个数.
解的个数.
 ,
, ,
,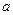 为常数.
为常数.(1) 求函数
 的定义域
的定义域 ;
;(2) 若
 时,对于
时,对于 ,比较
,比较 与
与 的大小;
的大小;(3) 讨论方程
 解的个数.
解的个数.解:(1)由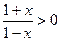 ,得:
,得: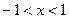 ,
,
∴函数 的定义域
的定义域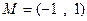 . ……………………………………3分
. ……………………………………3分
(2)令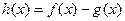 ,
,
则 时,
时,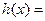
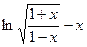 。
。
又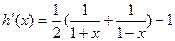
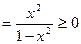
(仅在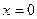 时,
时,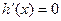 )
)
∴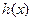 在
在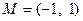 内是增函数, ……………………………………6分
内是增函数, ……………………………………6分
∴当 时,
时, ,
,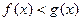 ;
;
当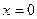 时,
时, 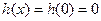 ,
, ;
;
当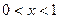 时,
时, 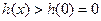 ,
,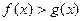 . ……………………………………8分
. ……………………………………8分
(3)讨论方程 解的个数,即讨论
解的个数,即讨论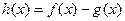 零点的个数.
零点的个数.
因为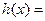
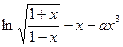 ,
,
所以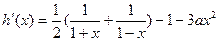
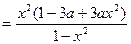
①当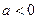 时,
时,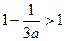 ,
,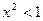 ,所以
,所以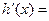
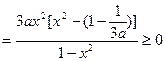
(仅在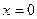 时,
时,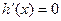 )
)
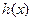 在
在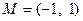 内是增函数,
内是增函数,
又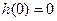 ,
,
所以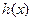 有唯一零点; ……………………………………9分
有唯一零点; ……………………………………9分
②当 时,由(2)知
时,由(2)知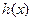 有唯一零点; ……………………………………10分
有唯一零点; ……………………………………10分
③当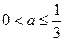 时,
时,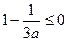 ,
,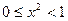
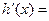
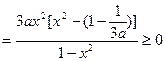 (仅在
(仅在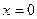 时,
时,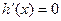 )
)
所以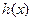 在
在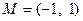 内是增函数,
内是增函数,
又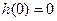 ,
,
所以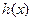 有唯一零点; ……………………………………11分
有唯一零点; ……………………………………11分
④当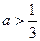 时,
时,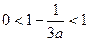 ,
,
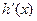

 ,或
,或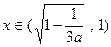 时,
时,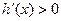 ,
,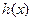 递增,
递增,
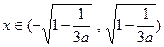 时,
时,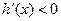 ,
,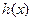 递减.
递减.
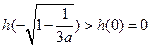 ,
, 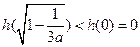 ;
;
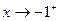 时,
时, 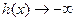 ;
; 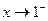 时,
时, 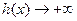 ,
,
∴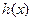 在区间
在区间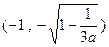 ,
,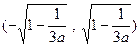 及
及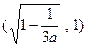 内各有一个零点.
内各有一个零点.
……………………………………13分
综上,当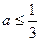 时,方程
时,方程 有唯一解;
有唯一解;
当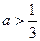 时,方程
时,方程 有三个解. ……………………………………14
有三个解. ……………………………………14
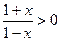 ,得:
,得: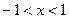 ,
, ∴函数
 的定义域
的定义域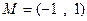 . ……………………………………3分
. ……………………………………3分(2)令
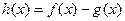 ,
,则
 时,
时,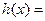
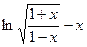 。
。又
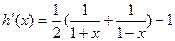
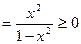
(仅在
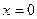 时,
时,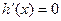 )
)∴
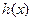 在
在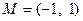 内是增函数, ……………………………………6分
内是增函数, ……………………………………6分∴当
 时,
时, ,
,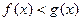 ;
;当
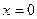 时,
时, 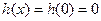 ,
, ;
; 当
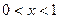 时,
时, 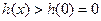 ,
,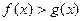 . ……………………………………8分
. ……………………………………8分(3)讨论方程
 解的个数,即讨论
解的个数,即讨论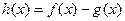 零点的个数.
零点的个数.因为
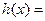
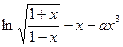 ,
,所以
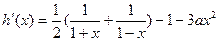
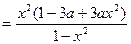
①当
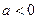 时,
时,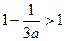 ,
,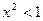 ,所以
,所以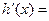
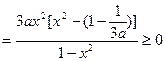
(仅在
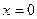 时,
时,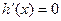 )
)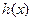 在
在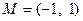 内是增函数,
内是增函数,又
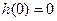 ,
,所以
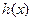 有唯一零点; ……………………………………9分
有唯一零点; ……………………………………9分②当
 时,由(2)知
时,由(2)知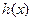 有唯一零点; ……………………………………10分
有唯一零点; ……………………………………10分③当
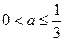 时,
时,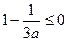 ,
,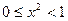
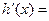
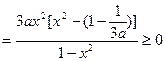 (仅在
(仅在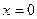 时,
时,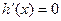 )
)所以
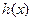 在
在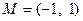 内是增函数,
内是增函数,又
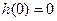 ,
,所以
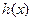 有唯一零点; ……………………………………11分
有唯一零点; ……………………………………11分④当
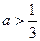 时,
时,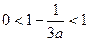 ,
,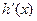

 ,或
,或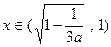 时,
时,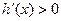 ,
,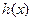 递增,
递增,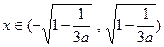 时,
时,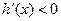 ,
,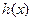 递减.
递减.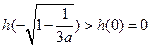 ,
, 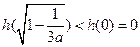 ;
;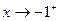 时,
时, 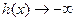 ;
; 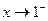 时,
时, 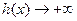 ,
,∴
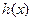 在区间
在区间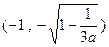 ,
,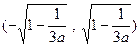 及
及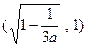 内各有一个零点.
内各有一个零点.……………………………………13分
综上,当
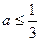 时,方程
时,方程 有唯一解;
有唯一解;当
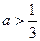 时,方程
时,方程 有三个解. ……………………………………14
有三个解. ……………………………………14略

练习册系列答案
相关题目
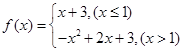 ,则函数
,则函数 的零点个数为( )
的零点个数为( ) ,函数
,函数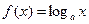 在区间
在区间 上的最大值与最小值之差为
上的最大值与最小值之差为 ,
, 的值为( )
的值为( )

 ,若
,若 ,则
,则
 是定义在R上的奇函数,当x≤0时,
是定义在R上的奇函数,当x≤0时, ,则
,则 .
.
 ,且
,且 ,则函数
,则函数 的值是 .
的值是 .
 是定义域上的连续函数,则实数
是定义域上的连续函数,则实数 .
. ,则
,则 的值为
的值为 .
. 
 .
. 
 .
. 
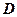 .
. 
