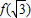题目内容
 如图,三次函数y=ax3+bx2+cx+d的零点为-1,1,2,则该函数的单调减区间为
如图,三次函数y=ax3+bx2+cx+d的零点为-1,1,2,则该函数的单调减区间为[
,
]
2-
| ||
| 3 |
2+
| ||
| 3 |
[
,
]
.2-
| ||
| 3 |
2+
| ||
| 3 |
分析:根据函数y=ax3+bx2+cx+d的零点为-1,1,2,建立函数关系式,从而求出函数y的解析式,最后解不等式y′(x)<0即可求出函数的单调减区间.
解答:解:∵函数y=ax3+bx2+cx+d的零点为-1,1,2,如图,
得y=a(x+1)(x-1)(x-2),且a>0,
y=a(x3-2x2-x+2),y'(x)=a(3x2-4x-1)=3a(x-
)(x-
),
令y′≤0得x∈[
,
]
则该函数的单调减区间为 [
,
].
故答案为:[
,
].
得y=a(x+1)(x-1)(x-2),且a>0,
y=a(x3-2x2-x+2),y'(x)=a(3x2-4x-1)=3a(x-
2-
| ||
| 3 |
2+
| ||
| 3 |
令y′≤0得x∈[
2-
| ||
| 3 |
2+
| ||
| 3 |
则该函数的单调减区间为 [
2-
| ||
| 3 |
2+
| ||
| 3 |
故答案为:[
2-
| ||
| 3 |
2+
| ||
| 3 |
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的极值和单调性等基础题知识,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
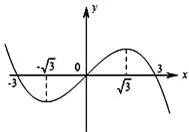 设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )
设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )A、f(x)的极大值为f(
| ||||
B、f(x)的极大值为f(-
| ||||
| C、f(x)的极大值为f(-3),极小值为f(3) | ||||
| D、f(x)的极大值为f(3),极小值为f(-3) |
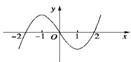 7、设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x•f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( )
7、设f(x)是一个三次函数,f′(x)为其导函数,如图所示的是y=x•f′(x)的图象的一部分,则f(x)的极大值与极小值分别是( ) 如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图已知O为坐标原点,∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
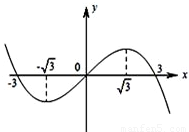 设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )
设三次函数f(x)的导函数为f′(x),函数y=x•f′(x)的图象的一部分如图所示,则正确的是( )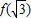 ,极小值为
,极小值为
 ,极小值为
,极小值为