题目内容
投掷两颗骰子,得到其向上的点数分别为m和n,则复数(m+ni)(n﹣mi)为实数的概率为( )
A.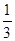 | B.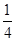 | C.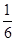 | D.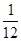 |
C
解析试题分析:因为(m+ni)(n-mi)=2mn+(n2-m2)i为实数,所以n2=m2,
故m=n则可以取1、2、3、4、5、6,共6种可能,
所以P= ,故选C.
,故选C.
考点:1.基本概念;2.古典概型及其概率计算公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,则
,则
A. | B.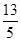 | C.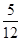 | D.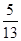 |
已知复数 ,则
,则  ( )
( )
A. | B.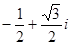 | C. | D. |
已知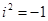 ,则
,则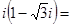 ( )
( )
A.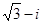 | B.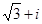 | C.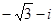 | D.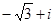 |
计算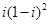 的值等于( )
的值等于( )
| A.-4 | B.2 | C.-2i | D.4i |
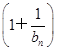 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与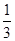 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.
 的值.
的值.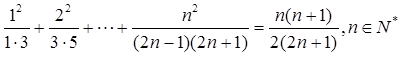
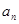 }满足
}满足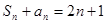 ,
,  ,并推测
,并推测