题目内容
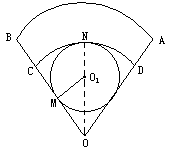
一扇形铁皮AOB,半径OA=72cm,圆心角∠AOB= ,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩余的扇形COD内剪下一个最大的圆刚好做容器的下底(圆台下底面大于上底面)(如图),则OC应取多少?
,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩余的扇形COD内剪下一个最大的圆刚好做容器的下底(圆台下底面大于上底面)(如图),则OC应取多少?
答案:
解析:
解析:
|
解:设OC=xcm,圆台下底面半径为r,即 说明:本题可以进而计算圆台形容器的最大容积及其侧面积等. |

练习册系列答案
相关题目
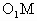 =r.∠CON=
=r.∠CON=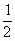 ∠AOB=
∠AOB=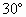 ,∴
,∴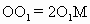 =2r,ON=
=2r,ON= =3r,∴r=
=3r,∴r=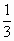 x.由2πr与
x.由2πr与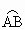 长相等得2πr=
长相等得2πr=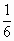 ·2π·72,∴r=12,故x=3r=36(cm).即OC应取36cm.
·2π·72,∴r=12,故x=3r=36(cm).即OC应取36cm. 如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形
如图,现有一块半径为2m,圆心角为90°的扇形铁皮AOB,欲从其中裁剪出一块内接五边形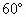 ,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为________.
,现剪下一个扇环ABCD做圆台形容器的侧面,并从剩下的扇形OCD内剪下一个最大的圆刚好做容器的下底(圆台的下底面大于上底面)(如图),则OC的长为________.