题目内容
已知点 在椭圆
在椭圆 上,则
上,则 的最大值为( )
的最大值为( )
A. B.-1 C.2 D.7
B.-1 C.2 D.7
【答案】
D
【解析】
试题分析:因为点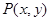 在椭圆
在椭圆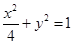 上,那么可知
上,那么可知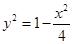 ,所以
,所以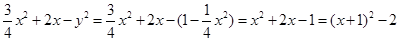 ,因为椭圆中-2
,因为椭圆中-2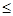 x
x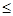 2,那么结合二次函数的性质可知函数的对称轴为x=-1,定义域为-2
2,那么结合二次函数的性质可知函数的对称轴为x=-1,定义域为-2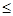 x
x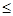 2,开口向上,那么可知当x=2时,函数值最大且为7.选D.
2,开口向上,那么可知当x=2时,函数值最大且为7.选D.
考点:本试题主要考查了椭圆上点满足关系式的最值问题。
点评:解决该试题的关键是可以运用椭圆的参数方程,运用三角函数式得到最值,也可以运用直角坐标结合椭圆 性质得到。

练习册系列答案
相关题目
 在椭圆
在椭圆 上,则
上,则 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 在椭圆
在椭圆 上,则
上,则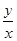 的最大值是( )
的最大值是( ) B、
B、 C、
C、 D、
D、