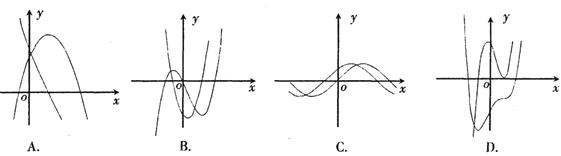
题目内容
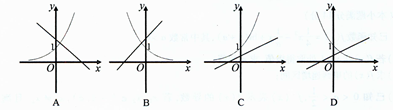
已知函数
是定义在
上的偶函数，且当
时，
，则函数
的大致图像为
是定义在上的偶函数，且当时，，则函数的大致图像为C
根据题意，先通过对称点的方法求出函数在区间（-∞，0）上的表达式，从而得出函数完整的表达式，然后利用对数函数y=lnx图象向左平移一个单位的图象与原函数在（0，+∞）上图象进行对照，得到正确的选项．
解：∵当x＞0时，f（x）=ln（x+1），
∴设x＜0，得-x＞0，f（-x）=ln（-x+1）
又∵函数f（x）是定义在R上的偶函数，
∴f（-x）=f（x）
即当x＜0时，f（x）=ln（-x+1）
综上所述，得f（x）=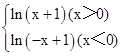
由自然对数的底为e=2.71828…＞1，当x＞0时原函数由对数函数y=lnx图象左移一个单位而来，
得当x＞0时函数为增函数，函数图象是上凸的
根据以上讨论，可得C选项符合条件
故选C
解：∵当x＞0时，f（x）=ln（x+1），
∴设x＜0，得-x＞0，f（-x）=ln（-x+1）
又∵函数f（x）是定义在R上的偶函数，
∴f（-x）=f（x）
即当x＜0时，f（x）=ln（-x+1）
综上所述，得f（x）=
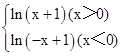
由自然对数的底为e=2.71828…＞1，当x＞0时原函数由对数函数y=lnx图象左移一个单位而来，
得当x＞0时函数为增函数，函数图象是上凸的
根据以上讨论，可得C选项符合条件
故选C
练习册系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
相关题目
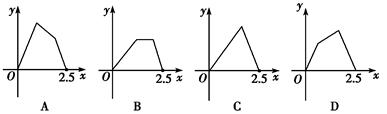
分别表示乌龟和兔子所行的路程，
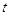为时间，则与故事情节相吻合是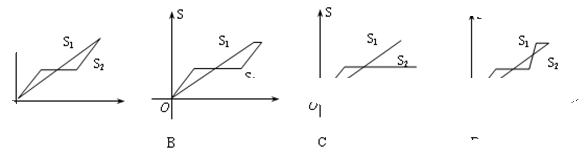 
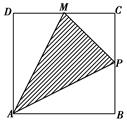
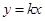与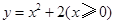
的图象相交于
，
，
，
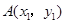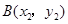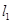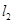分别是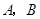
两点的切线，
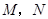分别是
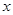轴的交点．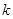
的取值范围；
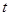为点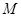
的横坐标，当
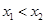时，写出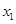
为自变量的函数式，并求其定义域和值域；
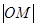与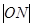
的大小，并说明理由（
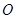是坐标原点）．
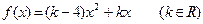，对任意实数
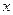，有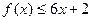
恒成立；数列
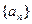满足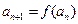
.
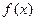的解析式和值域；
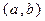，使得当
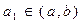时，数列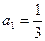
，是否存在非零整数
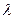，使得对任意
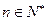，都有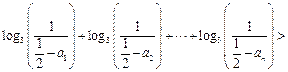
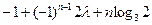恒成立，若存在，
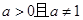时，函数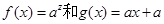
的图象只可能是（ ）
