Question

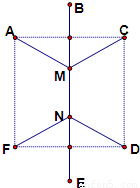
某大学为了发展需要，准备兴建新校区．新校区规划分南北两个校区，北区拟建A，B，C三个不同功能的教学小区，南区拟建D，E，F三个不同功能的生活小区．南北校区用一条中心主干道MN相连，各功能小区与中心主干道用支道相连，并且各功能小区到中心干道的端点的距离相等，A，C，D，F在边长为2公里的正方形顶点位置，B，E分别在MN的延长线上．已知中心主干道的造价为每公里30万元，支道造价为每公里20万元．问当中心主干道约为多少公里时，才能使道路总造价最低？道路总造价最低为多少万元？（ 参考数据

3

=1.732，结果保留三位有效数字）

Answer 1

分析：根据中心主干道的造价为每公里30万元，支道造价为每公里20万元，可得关于道路总造价的函数关系式，利用导数法可求最值．

解答：解：设MN=2x，O为正方形的中心，总造价为y万元…．（1分）
过M作MP⊥AF，垂足为P，则MP=1，AP=1-x，AM=

12+(1-x)2

=

x2-2x+2

…．（3分）
故y=6AM•20+MN•30=120

x2-2x+2

+60x…．（6分）y′=

120(x-1)

x2-2x+2

+60…．（8分）
令y′=0⇒2(1-x)=

x2-2x+2

∴3x2-6x+2=0 ∴x1=1-

3

3

，x2=1+

3

3

＞1（舍去）
当x∈(0，1-

3

3

)，y′＜0；x∈(1-

3

3

，1)，y′＞0…（12分）
故当x=1-

3

3

时，ymin=60(1+

3

)≈164（万元）
答：当中心主干道约为0.845公里时，才能使道路总造价最低．道路总造价最低约为164万元…．（14分）

点评：本题以实际问题为载体，考查函数模型的构建，考查利用导数判断函数单调性，从而求函数的最值．