题目内容
由某种设备的使用年限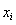 (年)与所支出的维修费
(年)与所支出的维修费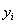 (万元)的数据资料,算得
(万元)的数据资料,算得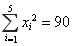 ,
, ,
, ,
, 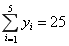 .
.
(Ⅰ)求所支出的维修费 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
;
(Ⅱ)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(Ⅲ)估计使用年限为8年时,支出的维修费约是多少.
附:在线性回归方程 中,
中, ,
, ,其中
,其中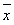 ,
, 为
为
样本平均值,线性回归方程也可写为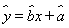 .
.
【答案】
(I)线性回归方程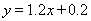 ;(II)正相关.;(Ⅲ)
;(II)正相关.;(Ⅲ)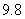 万元.
万元.
【解析】
试题分析:(Ⅰ)根据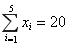 ,
, 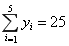 可得平均数;用所给公式
可得平均数;用所给公式 ,
, 可求得
可求得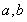 的值,从而得线性回归方程.(Ⅱ)若
的值,从而得线性回归方程.(Ⅱ)若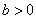 ,则为正相关;若
,则为正相关;若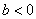 ,则为负相关; (Ⅲ)将
,则为负相关; (Ⅲ)将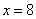 代入回归方程,所得函数值即为估计使用年限为8年时,支出的维修费.
代入回归方程,所得函数值即为估计使用年限为8年时,支出的维修费.
试题解析:(Ⅰ)
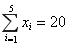 ,
, 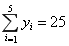 ,
,
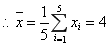 ,
, . (4分)
. (4分)
 , (7分)
, (7分)
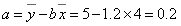 . (8分)
. (8分)
 线性回归方程
线性回归方程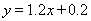 . (9分)
. (9分)
(Ⅱ)由(Ⅰ)知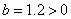 ,
,
 变量
变量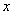 与
与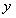 之间是正相关. (11分)
之间是正相关. (11分)
(Ⅲ)由(Ⅰ)知,当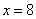 时,
时,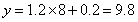 (万元),即估计使用年限为8年时,支出的维修费约是
(万元),即估计使用年限为8年时,支出的维修费约是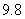 万元. (13分)
万元. (13分)
考点:线性回归方程及其应用.

练习册系列答案
相关题目
假设关于某种设备的使用年限x和支出的维修费用y(万元),有以下的统计资料:
若由资料知,y对x呈线性相关关系.
试求(1)线性回归方程y=bx+c的确回归系数a,b.
(2)估计使用年限为10年时,维修费用是多少?
参考公式:回归直线方程:y=bx+a.
.
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
试求(1)线性回归方程y=bx+c的确回归系数a,b.
(2)估计使用年限为10年时,维修费用是多少?
参考公式:回归直线方程:y=bx+a.
|
统计某单位某种设备的使用年限x和所需要的维修费用y(万元)得下表:
由表中数据计算出线性回归方程
=bx+a,其中b=1.23.据此预测使用10年的维修费用(单位:万元)为( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| ? |
| y |
| A、12.04 |
| B、12.31 |
| C、12.88 |
| D、12.38 |
假设关于某种设备的使用年限![]() 和支出的维修费用
和支出的维修费用![]() (万元),有以下的统计资料:
(万元),有以下的统计资料:
| 使用年限 | 2 | 3 | 4 | 5 | 6 |
| 维修费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,![]() 对
对![]() 呈线性相关关系。
呈线性相关关系。
试求(1)线性回归方程![]() 的确回归系数
的确回归系数![]() .
.
(2)估计使用年限为10年时,维修费用是多少?

