题目内容
函数 的图像与
的图像与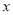 轴的交点至少有一个在原点的右侧.
轴的交点至少有一个在原点的右侧.
(1)求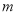 的取值范围;
的取值范围;
(2)对于(1)中的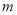 ,设
,设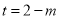 ,不等式
,不等式 恒成立,求
恒成立,求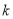 的取值范围(
的取值范围( 表示不超过
表示不超过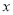 的最大整数).
的最大整数).
练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
题目内容
函数 的图像与
的图像与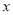 轴的交点至少有一个在原点的右侧.
轴的交点至少有一个在原点的右侧.
(1)求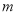 的取值范围;
的取值范围;
(2)对于(1)中的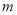 ,设
,设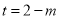 ,不等式
,不等式 恒成立,求
恒成立,求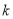 的取值范围(
的取值范围( 表示不超过
表示不超过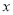 的最大整数).
的最大整数).
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案