题目内容
某工厂在政府的帮扶下,准备转型生产一种特殊机器,生产需要投入固定成本500万 元,生产与销售均以百台计数,且每生产100台,还需增加可变成本1000万元.若市场对该 产品的年需求量为500台,每生产m百台的实际销售收入近似满足函数R(m)=5000m-500m2(0≤m≤5,m∈N)(I)试写出第一年的销售利润y(万元)关于年产量x单位:百台,x≤5,x∈N*)的函数关系式;
(说明:销售利润=实际销售收人一成本)
(II )因技术等原因,第一年的年生产量不能超过300台,若第一年人员的年支出费用u(x)(万元)与年产量x(百台)的关系满足u(x)=500x+500(x≤3,x∈N*,问年产量X为多少百台时,工厂所得纯利润最大?
【答案】分析:(Ⅰ)利用销售利润=实际销售收人一成本,成本=固定成本+增加成本,即可得出;
(Ⅱ)利用工厂所得纯利润=工厂销售利润-人员的年支出费用,及二次函数的单调性即可得出.
解答:解:(Ⅰ),由题意可得,y=5000x-500x2-500-1000x,
即y=-500x2+4000x-500,(x≤5,x∈N*).
(Ⅱ)设工厂所得纯利润为h(x),则
h(x)=-500x2+4000x-500-u(x)
=-500x2+3500x-1000
=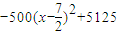 (x≤3,x∈N*).
(x≤3,x∈N*).
∴当x=3时,函数h(x)取得最大值h(3)=5000.
当年产量为3百台时,工厂所得纯利润最大,最大利润为5000万元.
点评:正确理解销售利润=实际销售收人一成本、成本=固定成本+增加成本、工厂所得纯利润=工厂销售利润-人员的年支出费用、二次函数的单调性是解题的关键.
(Ⅱ)利用工厂所得纯利润=工厂销售利润-人员的年支出费用,及二次函数的单调性即可得出.
解答:解:(Ⅰ),由题意可得,y=5000x-500x2-500-1000x,
即y=-500x2+4000x-500,(x≤5,x∈N*).
(Ⅱ)设工厂所得纯利润为h(x),则
h(x)=-500x2+4000x-500-u(x)
=-500x2+3500x-1000
=
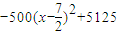 (x≤3,x∈N*).
(x≤3,x∈N*).∴当x=3时,函数h(x)取得最大值h(3)=5000.
当年产量为3百台时,工厂所得纯利润最大,最大利润为5000万元.
点评:正确理解销售利润=实际销售收人一成本、成本=固定成本+增加成本、工厂所得纯利润=工厂销售利润-人员的年支出费用、二次函数的单调性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目