题目内容
已知数列 中,
中, ,
, ,数列
,数列 中,
中, ,且点
,且点 在直线
在直线 上。
上。
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)若 ,求数列
,求数列 的前
的前 项和
项和 ;
;
【解析】第一问中利用数列的递推关系式
 ,因此得到数列
,因此得到数列 的通项公式;
的通项公式;
第二问中, 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列
得到其前n项和。
第三问中, 又
又 

 ,利用错位相减法得到。
,利用错位相减法得到。
解:(1)
 即数列
即数列 是以
是以 为首项,2为公比的等比数列
为首项,2为公比的等比数列

 ……4分
……4分
(2) 在
在 即为:
即为:
即数列 是以
是以 的等差数列
的等差数列

 ……8分
……8分
(3) 又
又 


 ①
①  ②
②
①- ②得到


【答案】
(1)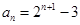 (2)
(2)
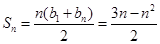
(3)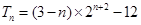

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 中,
中, ,则数列
,则数列 为 ( )
为 ( ) B.
B. C.
C. D.
D.
 中,
中, [来源:]
[来源:] 为等比数列;
为等比数列; 项的和为
项的和为 ,若
,若 ,求:正整数
,求:正整数