题目内容
如图,椭圆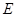 :
: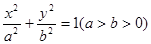 的右焦点
的右焦点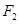 与抛物线
与抛物线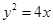 的焦点重合,过
的焦点重合,过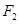 作与
作与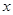 轴垂直的直线
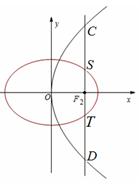
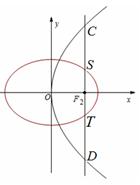
轴垂直的直线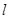 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且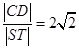 .
.
(Ⅰ)求椭圆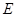 的方程;
的方程;
(Ⅱ)若过点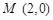 的直线与椭圆
的直线与椭圆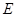 相交于两点
相交于两点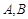 ,设
,设 为椭圆
为椭圆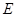 上一点,且满足
上一点,且满足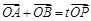 (
(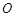 为坐标原点),当
为坐标原点),当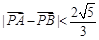 时,求实数
时,求实数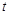 的取值范围.
的取值范围.
【答案】
(Ⅰ)由抛物线方程,得焦点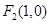 .
.
所以椭圆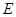 的方程为:
的方程为: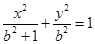 .
.
解方程组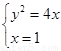 得C(1,2),D(1,-2). 由于抛物线、椭圆都关于x轴对称,
得C(1,2),D(1,-2). 由于抛物线、椭圆都关于x轴对称,
∴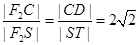 ,
,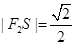 ,
∴
,
∴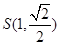 . …………2分
. …………2分
因此, ,解得
,解得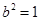 并推得
并推得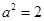 .
.
故椭圆的方程为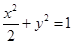 .
…………4分
.
…………4分
(Ⅱ)由题意知直线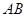 的斜率存在.
的斜率存在.
设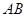 :
: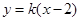 ,
,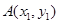 ,
,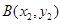 ,
,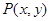 ,
,
由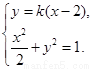 得
得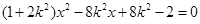 .
.
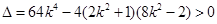 ,
,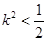 .…………6分
.…………6分
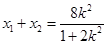 ,
,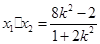 .
.
∵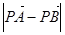 <
<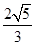 ,∴
,∴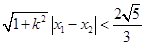 ,
,
∴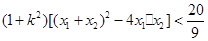 ∴
∴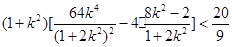 ,
,
∴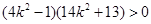 ,∴
,∴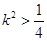 .∴
.∴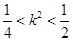 ,…………8分
,…………8分
∵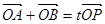 ,∴
,∴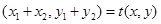 ,
,
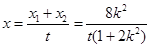 ,
,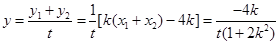 .
.
∵点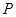 在椭圆上,∴
在椭圆上,∴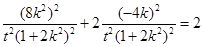 ,
,
∴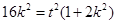 ∴
∴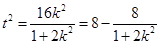 ,…………10分
,…………10分
∴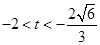 或
或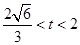 ,
,
∴实数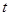 取值范围为
取值范围为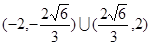 .
.
【解析】略

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
 :
: 的右焦点
的右焦点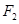 与抛物线
与抛物线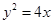 的焦点重合,过
的焦点重合,过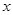 轴垂直的直线
轴垂直的直线 与椭圆交于S、T两点,与抛物线交于C、D两点,且
与椭圆交于S、T两点,与抛物线交于C、D两点,且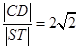 .
.
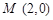 的直线与椭圆
的直线与椭圆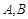 ,设
,设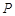 为椭圆
为椭圆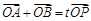 (
(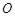 为坐标原点),当
为坐标原点),当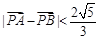 时,求实数
时,求实数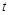 的取值范围.
的取值范围.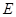 :
: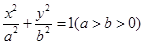 的左焦点为
的左焦点为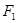 ,右焦点为
,右焦点为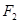 ,离心率
,离心率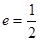 .过
.过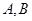 两点,且△
两点,且△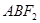 的周长为
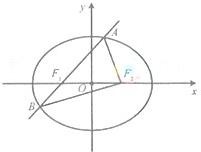
的周长为 .
.
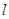 :
: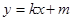 与椭圆
与椭圆 ,且与直线
,且与直线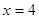 相交于点
相交于点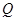 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点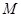 ,使得以
,使得以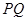 为直径的圆恒过点
为直径的圆恒过点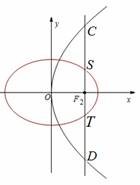 如图,椭圆
如图,椭圆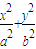 =1的两焦点F1,F2与短轴两端点B1,B2构成∠B2F1B1为120°,面积为
=1的两焦点F1,F2与短轴两端点B1,B2构成∠B2F1B1为120°,面积为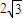 的菱形.
的菱形.