题目内容
某同学利用描点法画函数y=Asin(ωx+∅)(其中A>0,0<ω<2,-| π |
| 2 |
| π |
| 2 |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 0 | 1 | -1 | -2 |
分析:先由(0,1),(2,1)两组的数据的对称轴可知对称轴x=1,且可排除(1,0)更改为(1,A)代入可得,再根据(2,1),(3,-1)可得函数的一个对称中心(
,0),根据正弦函数相邻对称轴与对称中心距离为
这一性质可求ω,进一步求∅,A,即可.
| 5 |
| 2 |
| T |
| 4 |
解答:解:由题意可知(0,1),(2,1)关于对称轴对称,且对称轴x=1,
由三角函数的对称性可知,正弦函数在对称轴处取得最大值,且过(1,A),
从而可得第二組(1,0)错误
把(1,A)代入可得,ω+∅=
(2,1),(3,-1)关于(
,0)对称,所以可得(
,0)是函数的对称轴x=1相邻一个对称中心
从而函数的周期T=4×(
-1)=6,根据周期公式T=
=6,∴ω=
,∅=
函数f(x)=Asin(
x+
)
把函数图象上的点(0,1)代入函数解析式可得Asin
=1,∴A=2
故答案为:2sin(
x+
)
由三角函数的对称性可知,正弦函数在对称轴处取得最大值,且过(1,A),
从而可得第二組(1,0)错误
把(1,A)代入可得,ω+∅=
| π |
| 2 |
(2,1),(3,-1)关于(
| 5 |
| 2 |
| 5 |
| 2 |
从而函数的周期T=4×(
| 5 |
| 2 |
| 2π |
| ω |
| π |
| 3 |
| π |
| 6 |
函数f(x)=Asin(
| π |
| 3 |
| π |
| 6 |
把函数图象上的点(0,1)代入函数解析式可得Asin
| π |
| 6 |
故答案为:2sin(
| π |
| 3 |
| π |
| 6 |
点评:本题主要考查了利用正弦函数的对称性(轴对称、中心对称)求解函数的解析式,解决本题的关键是熟练掌握三角函数性质,要灵活运用三角函数的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某同学利用描点法画函数y=Asin(ωx+∅)(其中A>0,0<ω<2,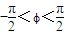 )的图象,列出的部分数据如表:
)的图象,列出的部分数据如表:
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+∅)的解析式应是y= .
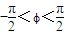 )的图象,列出的部分数据如表:
)的图象,列出的部分数据如表:| x | 1 | 2 | 3 | 4 | |
| y | 1 | 1 | -1 | -2 |
某同学利用描点法画函数y=Asin(ωx+∅)(其中A>0,0<ω<2,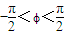 )的图象,列出的部分数据如表:
)的图象,列出的部分数据如表:
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+∅)的解析式应是y= .
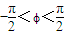 )的图象,列出的部分数据如表:
)的图象,列出的部分数据如表:| x | 1 | 2 | 3 | 4 | |
| y | 1 | 1 | -1 | -2 |
某同学利用描点法画函数y=Asin(ωx+∅)(其中A>0,0<ω<2,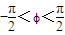 )的图象,列出的部分数据如表:
)的图象,列出的部分数据如表:
经检查,发现表格中恰有一组数据计算错误,请你根据上述信息推断函数y=Asin(ωx+∅)的解析式应是y= .
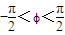 )的图象,列出的部分数据如表:
)的图象,列出的部分数据如表:| x | 1 | 2 | 3 | 4 | |
| y | 1 | 1 | -1 | -2 |