题目内容
已知复数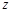 满足
满足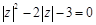 ,则复数
,则复数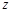 对应点的轨迹是 ( )
对应点的轨迹是 ( )
| A.1个圆 | B.线段 | C.2个点 | D.2个圆 |
A
解析试题分析:
根据复数z的模长满足|z|2-2|z|-3=0,把关于|z|的一元二次方程利用十字相乘法来分解,得到|z|的值,根据|z|的实际意义把不合题意的舍去,得到|z|=3,它表示以原点为中心,半径为3的圆解:∵复数z满足|z|2-2|z|-3=0,∴(|z|-3)(|z|+1)=0∴|z|=3或|z|=-1(舍),∴它表示以原点为中心,半径为3的圆.故选A.
考点:复数的模的求解
点评:本试题需要先对所给的复数的模长式子的整理,展开运算,结合复数的几何意义来得到,属于基础题。

练习册系列答案
相关题目
已知复数 等于
等于
A. | B.6 | C. | D. |
复数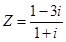 的实部是( )
的实部是( )
A.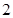 | B.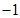 | C.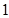 | D.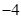 |
复数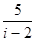 的共轭复数是
的共轭复数是
A.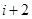 | B.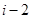 | C.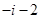 | D.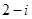 |
 为虚数单位,复数
为虚数单位,复数 的实部和虚部之和为
的实部和虚部之和为
| A.0 | B.1 | C.2 | D.3 |
复数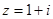 ,
,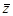 为
为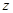 的共轭复数,则
的共轭复数,则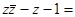 ( )
( )
| A.-2i | B.–i | C.i | D.2i |
设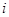 为虚数单位,则复数
为虚数单位,则复数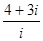 的虚部为 ( )
的虚部为 ( )
| A.-4 | B.-4i | C.4 | D.4i |
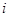 是虚数单位,复数
是虚数单位,复数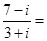 ( )
( )
A. | B.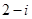 | C.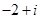 | D.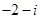 |
复数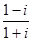 的共轭复数是
的共轭复数是
A.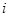 | B.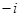 | C.1 | D.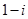 |