题目内容
(理科)定义在R上的函数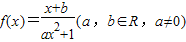 是奇函数,当且仅当x=1时,f(x)取得最大值.
是奇函数,当且仅当x=1时,f(x)取得最大值.(1)求a、b的值;
(2)若方程
 上有且仅有两个不同实根,求实数m的取值范围.
上有且仅有两个不同实根,求实数m的取值范围.
【答案】分析:(1)利用奇函数的定义f(-x)=-f(x)得b=0,通过对x的分段讨论求出函数的最大值,根据已知条件得到关于a的方程,求出a的值.
(2)将f(x)代入方程并将方程变形,将方程根的情况转换为二次方程的实根分布问题,结合二次函数的图象写出限制条件,求出m的范围.
解答:解:(1)由f(-x)=-f(x)得b=0
∴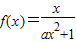
又由函数f(x)的定义域为R知a≥0
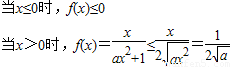
当且仅当ax2=1即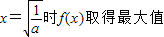
∴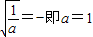
综上a=1,b=0…(6分)
(2)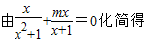

∴方程mx2+x+m+1=0在区间(-1,1)上有且仅有一个非零实根.
当m=0时,x=-1不合题意当m≠0时,分两种情况讨论
①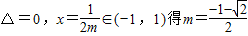
②令h(x)=mx2+x+m+1则h(-1)•h(1)<0且h(0)≠0解得-1<m<0
综上所述实数m的取值范围为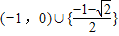 …(13分)
…(13分)
点评:本题考查二次方程的实根分布问题,应该结合二次函数的图象,从对称轴与区间的位置关系、区间端点值的符号限制.
(2)将f(x)代入方程并将方程变形,将方程根的情况转换为二次方程的实根分布问题,结合二次函数的图象写出限制条件,求出m的范围.
解答:解:(1)由f(-x)=-f(x)得b=0
∴
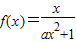
又由函数f(x)的定义域为R知a≥0
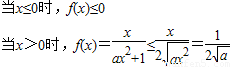
当且仅当ax2=1即
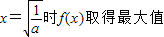
∴
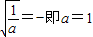
综上a=1,b=0…(6分)
(2)
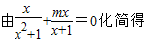

∴方程mx2+x+m+1=0在区间(-1,1)上有且仅有一个非零实根.
当m=0时,x=-1不合题意当m≠0时,分两种情况讨论
①
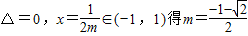
②令h(x)=mx2+x+m+1则h(-1)•h(1)<0且h(0)≠0解得-1<m<0
综上所述实数m的取值范围为
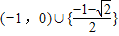 …(13分)
…(13分)点评:本题考查二次方程的实根分布问题,应该结合二次函数的图象,从对称轴与区间的位置关系、区间端点值的符号限制.

练习册系列答案
相关题目
 ,则f(2013)的值为 .
,则f(2013)的值为 . ,则f(2013)的值为 .
,则f(2013)的值为 . 是奇函数,当且仅当x=1时,f(x)取得最大值.
是奇函数,当且仅当x=1时,f(x)取得最大值. 上有且仅有两个不同实根,求实数m的取值范围.
上有且仅有两个不同实根,求实数m的取值范围.