题目内容
已知函数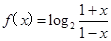 ,(x∈(- 1,1).
,(x∈(- 1,1).
(Ⅰ)判断f(x)的奇偶性,并证明;
(Ⅱ)判断f(x)在(- 1,1)上的单调性,并证明.
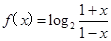 ,(x∈(- 1,1).
,(x∈(- 1,1).(Ⅰ)判断f(x)的奇偶性,并证明;
(Ⅱ)判断f(x)在(- 1,1)上的单调性,并证明.
证明:(Ⅰ)
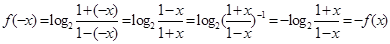
又x∈(-1,1),所以函数f(x)是奇函数
(Ⅱ)设 -1<x<1,△x=x2- x1>0
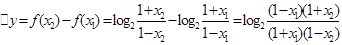
因为1- x1>1- x2>0;1+x2>1+x1>0
所以
所以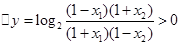
所以函数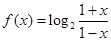 在(- 1,1)上是增函数
在(- 1,1)上是增函数
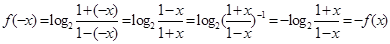
又x∈(-1,1),所以函数f(x)是奇函数
(Ⅱ)设 -1<x<1,△x=x2- x1>0
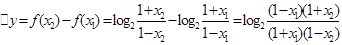
因为1- x1>1- x2>0;1+x2>1+x1>0
所以

所以
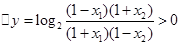
所以函数
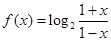 在(- 1,1)上是增函数
在(- 1,1)上是增函数略

练习册系列答案
相关题目
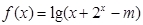 在区间
在区间 上有意义,则实数
上有意义,则实数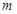 的取值范围是( )
的取值范围是( )


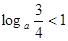
 ,求实数
,求实数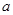 的取值范围。
的取值范围。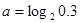 ,
, ,
, ,则有( )
,则有( )



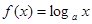
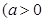 且
且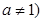 ,若
,若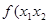 …
…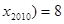 ,则
,则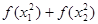 +…
+…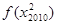 的值为( )
的值为( )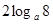
 在区间
在区间 上是减函数,则实数
上是减函数,则实数 的取值范围是 .
的取值范围是 . 0.3,则 ( )
0.3,则 ( )


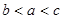
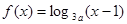 满足
满足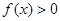 ,则
,则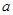 的取值范围是 ;
的取值范围是 ;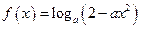 在
在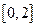 上单调递增,则实数
上单调递增,则实数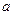 的取值范围为
的取值范围为