题目内容
袋中有8个除颜色不同其他都相同的球,其中1个为黑球,2个为白球,5个为红球.
(1)如果从袋中摸出2个球,求所摸出的2个球颜色不同的概率;
(2)如果从袋中一次摸出3个球,记得到红球的个数为X,求随机变量数学期望E(X).
解:(1)由题意知本题是一个等可能事件的概率
记“所摸出的2个球颜色不同”为事件A,
摸出的2个球颜色不同的种数是17种,
从8个球中摸出2个球不同的摸法有C82=28,
∴P(A)=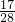
(2)∵符合条件的摸法包括下列四种,
一是3个球中没有红球只有一种摸法,
二是三个球中有1个红球,有C51C31=15种结果,
三是3个球中有2个红球,有C52C31=30,
四是3个球都是红球,有C53=10种结果,
由题意知变量X可能的取值是0、1、2、3,
P(X=0)=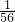 ,
,
P(X=1)=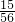 ,
,
P(X=2)=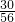
P(X=3)=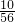
∴EX=0×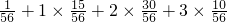 =
=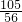
分析:(1)由题意知本题是一个等可能事件的概率,试验发生包含的所有事件是从8个球中选两个,而满足条件的事件是摸出的2个球颜色不同,写出事件的概率.
(2)从袋中一次摸出3个球,记得到红球的个数为X,由题意知X的可能取值是0、1、2、3,结合变量对应的事件写出变量对应事件的概率,算出期望.
点评:本题是一个等可能事件的概率和离散型随机变量的期望问题,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,是可以得满分的一道题目.
记“所摸出的2个球颜色不同”为事件A,
摸出的2个球颜色不同的种数是17种,
从8个球中摸出2个球不同的摸法有C82=28,
∴P(A)=
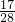
(2)∵符合条件的摸法包括下列四种,
一是3个球中没有红球只有一种摸法,
二是三个球中有1个红球,有C51C31=15种结果,
三是3个球中有2个红球,有C52C31=30,
四是3个球都是红球,有C53=10种结果,
由题意知变量X可能的取值是0、1、2、3,
P(X=0)=
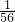 ,
,P(X=1)=
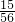 ,
,P(X=2)=
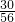
P(X=3)=
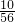
∴EX=0×
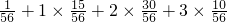 =
=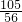
分析:(1)由题意知本题是一个等可能事件的概率,试验发生包含的所有事件是从8个球中选两个,而满足条件的事件是摸出的2个球颜色不同,写出事件的概率.
(2)从袋中一次摸出3个球,记得到红球的个数为X,由题意知X的可能取值是0、1、2、3,结合变量对应的事件写出变量对应事件的概率,算出期望.
点评:本题是一个等可能事件的概率和离散型随机变量的期望问题,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,是可以得满分的一道题目.

练习册系列答案
相关题目