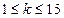题目内容
设正实数 满足
满足 ,则当
,则当 取得最大小值时,
取得最大小值时, 的最大值为( )
的最大值为( )
| A.0 | B.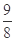 | C.2 | D. |
C
解析试题分析:因为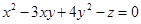 ,所以
,所以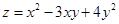 ,又因为
,又因为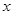 、
、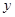 、
、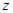 为正实数,
为正实数,
所以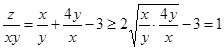 ,当且仅当
,当且仅当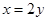 时取等号,即
时取等号,即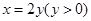 ,
,
所以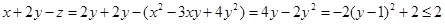 ,
,
所以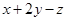 的最大值为2,故选C.
的最大值为2,故选C.
考点:用基本不等式求最值,配方法.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
下列各式中,最小值等于2的是( )
A.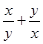 | B. | C. | D. |
设a>0,b>0,则以下不等式中不一定成立的是( )
| A.a2+b2+2≥2a+2b | B.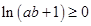 |
C.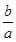 + +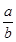 ≥2 ≥2 | D.a3+b3≥2ab2 |
已知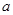 、
、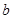 都是正实数,函数
都是正实数,函数 的图象过
的图象过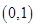 点,则
点,则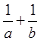 的最小值是( )
的最小值是( )
A.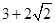 | B.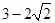 | C.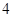 | D. |
设 ,
, ,若
,若 ,则
,则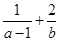 的最小值为( )
的最小值为( )
A.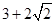 | B.6 | C. | D. |
设x,y∈R,a>1,b>1,若ax=by=2,a+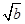 =4,则
=4,则 +
+ 的最大值为( )
的最大值为( )
| A.4 | B.3 | C.2 | D.1 |
小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则( )
A.a<v<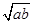 | B.v=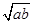 |
C.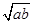 <v< <v<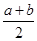 | D.v=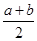 |
若点P(a,b)在直线x+y=2上,且在第一象限内,则ab+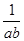 的最小值为( )
的最小值为( )
| A.2 | B.3 | C.4 | D.2 |
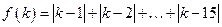 ,
,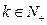 且
且