题目内容
把正偶数数列{2n}中的数按上小下大、左小右大的原则排成如下图“三角形”数表所示.设aij(i,j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数.(Ⅰ)若amn=2006,求m、n的值;
(Ⅱ)已知函数f(x)的反函数为f-1(x)=8nx3+n(x>0),若记三角形数表中从上往下数第n行各数的和为bn,求数列{f(bn)}的前n项和Sn.

解:(Ⅰ)∵三角形数表中前m行共有1+2+3+…+m=![]() 个数,
个数,
∴第m行最后一个数应当是所给数列中的第![]() 项.
项.
故第m行最后一个数是2·![]() =m2+m
=m2+m
因此,使得amn=2006的m是不等式m2+m≥2006的最小正整数解.
由m2+m≥2006得m2+m-2006≥0
∴m≥![]() =44
=44
∴m=45
于是,第45行第一个数是442+44+2=1 982
∴n=![]() +l=13
+l=13
(Ⅱ)∵f-1(x)=8nx3+n=y(x>0),
∴x=![]() .故f(x)=
.故f(x)=![]() (x>0)
(x>0)
∵第n行最后一个数是n2+n,且有n个数,若将n2+n看成第n行第一个数,
则第n行各数成公差为-2的等差数列,
故bn=n(n2+n)+![]() (-2)=n3+n.
(-2)=n3+n.
∴f(bn)=![]()
故Sn=![]()
∵![]() ,
,
两式相减得:
![]() Sn=
Sn=![]() +(
+(![]() )2+(
)2+(![]() )3+…+(
)3+…+(![]() )n-n(
)n-n(![]() )n+1=
)n+1=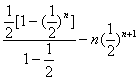
=1-(![]() )n-n(
)n-n(![]() )n+1
)n+1
∴Sn=2-(n+2)(![]() )n
)n

练习册系列答案
相关题目
 把正偶数数列{2n}的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第I行,从左往右数第J个数,若amn=2010,则
把正偶数数列{2n}的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表,设aij(i,j∈N*)是位于这个三角形数表中从上往下数第I行,从左往右数第J个数,若amn=2010,则 把正偶数数列{2n}中的数按上小下大、左小右大的原则排成如下三角形数表:
把正偶数数列{2n}中的数按上小下大、左小右大的原则排成如下三角形数表:
 ,(n∈N*)求数列{cn}的前n项和Sn.
,(n∈N*)求数列{cn}的前n项和Sn.