题目内容
已知函数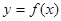 的定义域为R,对任意
的定义域为R,对任意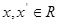 ,均有
,均有
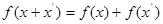 ,且对任意
,且对任意 都有
都有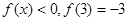 。
。
(1)试证明:函数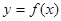 在R上是单调函数;
在R上是单调函数;
(2)判断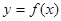 的奇偶性,并证明。
的奇偶性,并证明。
(3)解不等式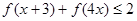 。
。
(4)试求函数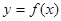 在
在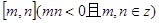 上的值域;
上的值域;
【答案】
(1)证明略
(2)奇函数,证明略
(3)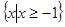
(4)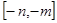
【解析】(1)任取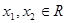 ,令
,令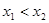
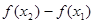
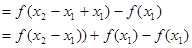
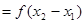 ……………………………………………2分
……………………………………………2分
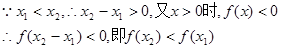
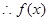 在R上是单调减函数
……………………………………………4分
在R上是单调减函数
……………………………………………4分
(2)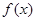 为奇函数,令
为奇函数,令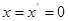 ,有
,有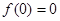 …………………………5分
…………………………5分
令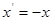 ,有
,有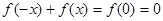
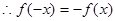 ………………………………………………7分
………………………………………………7分
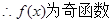 ……………………………………………8分
……………………………………………8分
(3)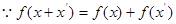
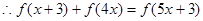
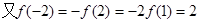 ………………………………………9分
………………………………………9分
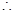 原不等式为:
原不等式为: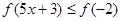 ……………………………………10分
……………………………………10分
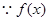 在R上递减,
在R上递减,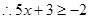
 不等式的解集为
不等式的解集为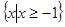 …………………………………11分
…………………………………11分
(4)由题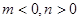
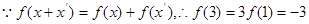
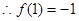
又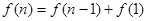
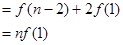
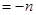 ………………………………………………………12分
………………………………………………………12分
由(2)知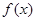 为奇函数,
为奇函数,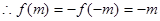 …………………13分
…………………13分
由(1)知,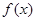 在
在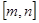 上递减,
上递减,
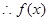 的值域为
的值域为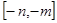 …………………………………………14分
…………………………………………14分

练习册系列答案
相关题目
 的定义域为R,且当
的定义域为R,且当 时,
时, 恒成立,
恒成立, 对称;
对称; 图象的一个对称点。
图象的一个对称点。 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且
 N*),则
N*),则 的值为( )
的值为( ) 的定义域为R,它的反函数为
的定义域为R,它的反函数为 ,如果
,如果 与
与 互为反函数,且
互为反函数,且 ,则
,则 的值为(
)
的值为(
) B、0
C、
B、0
C、 D、
D、
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意的实数
,且对任意的实数 R,等式
R,等式 成立.若数列
成立.若数列 满足
满足 ,且
,且 (
( N*),则
N*),则 的值为( )
的值为( )