题目内容
 如图,给定由10个点(任意相邻两点距离为1)组成的 正三角形点阵,在其中任意取三个点,以这三个点为顶 点构成的正三角形的个数是
如图,给定由10个点(任意相邻两点距离为1)组成的 正三角形点阵,在其中任意取三个点,以这三个点为顶 点构成的正三角形的个数是
- A.13
- B.14
- C.15
- D.17
A
分析:按边长分为1,2,3共3类,分别计算出个数即可.
解答:如图所示,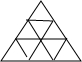
边长为1的正三角形共有1+3+5=9个;
边长为2的正三角形共有3个;
边长为3的正三角形共有1个.
综上可知:共有9+3+1=13个.
故选A.
点评:正确按边长分类是解题的关键.
分析:按边长分为1,2,3共3类,分别计算出个数即可.
解答:如图所示,

边长为1的正三角形共有1+3+5=9个;
边长为2的正三角形共有3个;
边长为3的正三角形共有1个.
综上可知:共有9+3+1=13个.
故选A.
点评:正确按边长分类是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
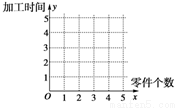
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
|
零件的个数x(个) |
2 |
3 |
4 |
5 |
|
加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程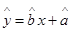 ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工10个零件需要多少时间?
(注: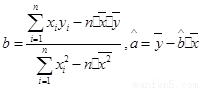 )
)
【解析】第一问中利用数据描绘出散点图即可
第二问中,由表中数据得 =52.5,
=52.5, 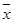 =3.5,
=3.5, =3.5,
=3.5,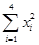 =54,∴
=54,∴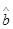 =0.7,
=0.7,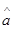 =1.05得到回归方程。
=1.05得到回归方程。
第三问中,将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时)得到结论。
(1)散点图如下图.
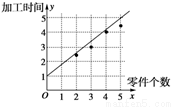 ………………4分
………………4分
(2)由表中数据得 =52.5,
=52.5, 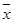 =3.5,
=3.5, =3.5,
=3.5,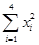 =54,
=54,
∴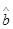 =…=0.7,
=…=0.7,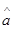 =…=1.05.
=…=1.05.
∴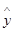 =0.7x+1.05.回归直线如图中所示.………………8分
=0.7x+1.05.回归直线如图中所示.………………8分
(3)将x=10代入回归直线方程,得y=0.7×10+1.05=8.05(小时),
∴预测加工10个零件需要8.05小时
 (2013•嘉兴一模)如图,给定由10个点(任意相邻两点距离为1)组成的 正三角形点阵,在其中任意取三个点,以这三个点为顶 点构成的正三角形的个数是( )
(2013•嘉兴一模)如图,给定由10个点(任意相邻两点距离为1)组成的 正三角形点阵,在其中任意取三个点,以这三个点为顶 点构成的正三角形的个数是( )
